Arithmétique ( PGCD )
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdibj
- Membre Naturel
- Messages: 67
- Enregistré le: 15 Sep 2017, 20:04
-
 par mehdibj » 03 Oct 2017, 21:21
par mehdibj » 03 Oct 2017, 21:21
salut , j'ai du mal a comprendre la deuxième partie du problème suivant :
on considére la suite
_{n\epsilon N})
definie par
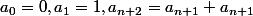
1) montrer que pour tout n

N et tout m

N*
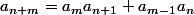
(celle la je l'ai démontrée)
2)en déduire que pour tout n

N* et m

N*
PGCD(
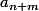
,

)=PGCD(
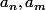
)
puis
=PGCD(a_{n},a_{r}))
où r est le reste de la division euclidienne de m par n
merci d'avence


-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 03 Oct 2017, 21:29
par infernaleur » 03 Oct 2017, 21:29
Salut,
Ta pas eue une autre question avant qui dit que pour tout n dans N* ,

et
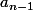
sont premier entre eux ?
Si oui tu peux montrer que les deux Pgcd ce divisent entre eux
i.e.
 / PGCD(a_{n},a_{m}))
et
/PGCD(a_{n+m},a_{n}))
-
mehdibj
- Membre Naturel
- Messages: 67
- Enregistré le: 15 Sep 2017, 20:04
-
 par mehdibj » 03 Oct 2017, 21:42
par mehdibj » 03 Oct 2017, 21:42
infernaleur a écrit:Salut,
Ta pas eue une autre question avant qui dit que pour tout n dans N* ,

et
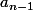
sont premier entre eux ?
Si oui tu peux montrer que les deux Pgcd ce divisent entre eux
i.e.
 / PGCD(a_{n},a_{m}))
et
/PGCD(a_{n+m},a_{n}))
si si j'ai déja demontrer que

et

mais je ne vois vraiment pas comment démontrer ce que tu viens de dire
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 03 Oct 2017, 21:47
par infernaleur » 03 Oct 2017, 21:47
Alors on pose
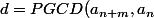)
et
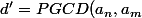)
On doit montrer que d divise d' et d' divise d.
Montrons pour commencer que d' divise d ( c'est le sens le plus facile)
Je te laisse essayer.
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 03 Oct 2017, 21:48
par infernaleur » 03 Oct 2017, 21:48
tu dois utiliser cette caractérisation :
Soient a,b,c des entiers.
Si ) , alors :
, alors :
i) d est le plus grand diviseur tel que d divise a et d divise b
ii) si c divise a et c divise b alors c divise d (c'est surtout ce point qui est le plus important dans la manipulation du pgcd)
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 03 Oct 2017, 21:58
par Pseuda » 03 Oct 2017, 21:58
Bonsoir,
Pour montrer que pgcd(x,y)=pgcd(z,t), on peut aussi montrer que : si un entier d divise x et y, alors il divise z et t, et que si un entier d divise z et t, alors il divise x et y.
(Cela voudra dire que l'ensemble des diviseurs de x et y est l'ensemble des diviseurs de z et t, et donc que le plus grand est le même.)
-
mehdibj
- Membre Naturel
- Messages: 67
- Enregistré le: 15 Sep 2017, 20:04
-
 par mehdibj » 03 Oct 2017, 22:08
par mehdibj » 03 Oct 2017, 22:08
infernaleur a écrit:Alors on pose
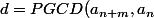)
et
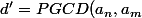)
On doit montrer que d divise d' et d' divise d.
Montrons pour commencer que d' divise d ( c'est le sens le plus facile)
Je te laisse essayer.
d' divise

d' divise
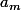
donc d' divise
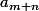
et d' divise

d'où d' divise PGCD (

,
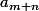
)
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 03 Oct 2017, 22:08
par infernaleur » 03 Oct 2017, 22:08
Pseuda a écrit:Bonsoir,
Pour montrer que pgcd(x,y)=pgcd(z,t), on peut aussi montrer que : si un entier d divise x et y, alors il divise z et t, et que si un entier d divise z et t, alors il divise x et y.
(Cela voudra dire que l'ensemble des diviseurs de x et y est l'ensemble des diviseurs de z et t, et donc que le plus grand est le même.)
Oui voilà je voulais qu'il voit sa tout seul mais c'est bien la où je voulais en venir ^^ (c'est pour sa j'ai énoncé cette caractérisation pour le mettre dans cette voie)
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 03 Oct 2017, 22:10
par infernaleur » 03 Oct 2017, 22:10
mehdibj a écrit: infernaleur a écrit:Alors on pose
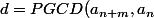)
et
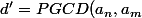)
On doit montrer que d divise d' et d' divise d.
Montrons pour commencer que d' divise d ( c'est le sens le plus facile)
Je te laisse essayer.
d' divise

d' divise
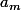
donc d' divise
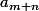 (*)
(*) et d' divise

d'où d' divise PGCD (

,
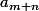
)
Exactement juste dans la ligne ou j'ai mis (*) justifie un petit peu.
Tu dis comme d' divise

et d' divise
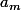
alors par combinaison linéaire d' divise
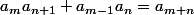
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 03 Oct 2017, 22:11
par infernaleur » 03 Oct 2017, 22:11
Bref ta montré que d' divise d bien joué.
Maintenant essaye de voir si d divise d'.
-
mehdibj
- Membre Naturel
- Messages: 67
- Enregistré le: 15 Sep 2017, 20:04
-
 par mehdibj » 03 Oct 2017, 22:22
par mehdibj » 03 Oct 2017, 22:22
infernaleur a écrit:Bref ta montré que d' divise d bien joué.
Maintenant essaye de voir si d divise d'.
je pense que c'est a peu pres le méme raisonement on a
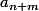
-
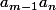
=
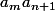
on a d divise
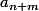
d divise

par combinaison linéaire d divise
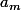
et d divise

d'où d divise d' ?
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 03 Oct 2017, 22:32
par infernaleur » 03 Oct 2017, 22:32
mehdibj a écrit: infernaleur a écrit:Bref ta montré que d' divise d bien joué.
Maintenant essaye de voir si d divise d'.
je pense que c'est a peu pres le méme raisonement on a
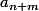
-
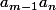
=
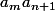
on a d divise
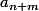
d divise
 par combinaison linéaire d divise
par combinaison linéaire d divise 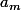
et d divise

d'où d divise d' ?
Attention !!!!
C'est faux c'est : d divise
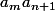
tu ne peux pas en dire plus (sa aurait été bien trop beau ^^).
Mais en effet on va se remmener à d divise
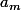
mais ce n'est pas si évident que sa il faut le montrer .
Donc si je récapitule on à d divise
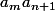
Mais tu ma dis que tu avais montré que
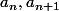
sont premiers entre eux
Donc que peux tu dire de d et

???
-
mehdibj
- Membre Naturel
- Messages: 67
- Enregistré le: 15 Sep 2017, 20:04
-
 par mehdibj » 03 Oct 2017, 22:40
par mehdibj » 03 Oct 2017, 22:40
infernaleur a écrit: mehdibj a écrit: infernaleur a écrit:Bref ta montré que d' divise d bien joué.
Maintenant essaye de voir si d divise d'.
je pense que c'est a peu pres le méme raisonement on a
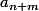
-
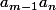
=
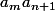
on a d divise
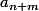
d divise
 par combinaison linéaire d divise
par combinaison linéaire d divise 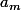
et d divise

d'où d divise d' ?
Attention !!!!
C'est faux c'est : d divise
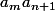
tu ne peux pas en dire plus (sa aurait été bien trop beau ^^).
Mais en effet on va se remmener à d divise
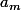
mais ce n'est pas si évident que sa il faut le montrer .
Donc si je récapitule on à d divise
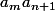
Mais tu ma dis que tu avais montré que
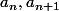
sont premiers entre eux
Donc que peux tu dire de d et

???
oui oui j'avais oublier de mentionné que

et

sont premiers entre eux
et puisque d divise

donc d divise
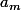
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 03 Oct 2017, 22:45
par infernaleur » 03 Oct 2017, 22:45
qu'est ce qui fait que :
Si

et

sont premiers entre eux et d divise

alors
d divise
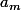
???
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 03 Oct 2017, 22:47
par infernaleur » 03 Oct 2017, 22:47
Ta conclusion est trop rapide il manque des étapes ...
-
mehdibj
- Membre Naturel
- Messages: 67
- Enregistré le: 15 Sep 2017, 20:04
-
 par mehdibj » 03 Oct 2017, 22:57
par mehdibj » 03 Oct 2017, 22:57
infernaleur a écrit:qu'est ce qui fait que :
Si

et

sont premiers entre eux et d divise

alors
d divise
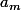
???
il manque la partie où je doit dire " donc d ne divise pas

"
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 03 Oct 2017, 23:03
par infernaleur » 03 Oct 2017, 23:03
Oui et plus précisément ce qu'il faut dire principalement est que d et

sont
premiers entre eux !!!
Donc comme d divise
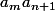
et d et

sont premiers entre eux.
D'après le lemme de Gauss :
d divise
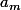
(c'est ce théorème que j'attendais que tu énonce ).
Ce qui conclut ton exercice.
-
mehdibj
- Membre Naturel
- Messages: 67
- Enregistré le: 15 Sep 2017, 20:04
-
 par mehdibj » 03 Oct 2017, 23:05
par mehdibj » 03 Oct 2017, 23:05
infernaleur a écrit:Oui et plus précisément ce qu'il faut dire principalement est que d et

sont
premiers entre eux !!!
Donc comme d divise
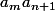
et d et

sont premiers entre eux.
D'après le lemme de Gauss :
d divise
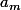
(c'est ce théorème que j'attendais que tu énonce ).
Ce qui conclut ton exercice.
merci . c'est pas mon jour aujourd’hui


-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 03 Oct 2017, 23:07
par infernaleur » 03 Oct 2017, 23:07
T'inquiète pas c'est pas un exo évident, y'a beaucoup de chose à vérifier et faut omettre aucune hypothèse.
Bonne nuit à toi en tout cas et à bientôt !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
et
sont premier entre eux ?
 / PGCD(a_{n},a_{m}))
et
et
(*)
,
)
-
=
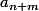

-
=
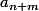

tu ne peux pas en dire plus (sa aurait été bien trop beau ^^).
mais ce n'est pas si évident que sa il faut le montrer .
sont premiers entre eux
???
et
sont premiers entre eux et d divise
???
sont premiers entre eux !!!
et d et
sont premiers entre eux.
(c'est ce théorème que j'attendais que tu énonce ).

