Arithmétique flottante
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
par legeniedesalpages » 13 Nov 2007, 14:16
Bonjour,
j'ai du mal avec cet exercice:
On note
)
l'ensemble des flottants en base 2 avec un exposant (en base 2) à 8 bits (décimales binaires) et une mantisse à 23 bits.
Donc cet ensemble correspond au format IEEE à 32 bits (simple précision).
Préciser, le plus petit flottant
tel que
puis comment trouver la distance entre deux flottants successifs.
Je sais bien que
, mais je ne vois pas comment le montrer.
Ensuite, pour déterminer la distance entre deux flottants successifs, je n'ai aucune idée de comment procéder.
Merci pour votre aide.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
par ThSQ » 13 Nov 2007, 18:42
Doit manquer le bit de signe non :nerf: ?
Plus sérieux, l'écart entre deux flottants succéssifs est augmenté d'un facteur 2 tous les 2^23.
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
par Imod » 13 Nov 2007, 18:56
Désolé si l'humour est un peu lourd , mais là , je coule :mur:
Imod
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
par ThSQ » 13 Nov 2007, 19:18
Imod a écrit:Désolé si l'humour est un peu lourd , mais là , je coule :mur:
Imod
:help: (j'ai pas compris Imod, chuis un peu naze là faut dire)
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
par Imod » 13 Nov 2007, 19:21
ThSQ a écrit::help: (j'ai pas compris Imod, chuis un peu naze là faut dire)
Tout ce qui ne flotte pas ... :--:
Imod
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
par ThSQ » 13 Nov 2007, 21:02
Imod a écrit:Tout ce qui ne flotte pas ... :--:
'tin trop fort :we:
J'y étais pas là .... :marteau:
par legeniedesalpages » 13 Nov 2007, 22:14
ah oui effectivement,
j'ai trouvé ça aussi en allant au boulot, merci.
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
par Imod » 13 Nov 2007, 23:02
legeniedesalpages a écrit:ah oui effectivement, j'ai trouvé ça aussi en allant au boulot, merci.
Bon , j'annonçais la couleur au départ ( un peu lourd ) , je ne sais pas si le problème est compliqué mais le jargon me dépasse : je vous laisse travailler :we:
Imod
par legeniedesalpages » 14 Nov 2007, 00:23
là, je ne comprends pas vraiment comment il faut procéder:
On considère l'ensemble des flottants
)
, où donc l'exposant est à
bits, et la mantisse à
bits.
On note
)
la projection par arrondi sur
de
.
"Montrer" que
-x|}{|x|}\leq \frac{1}{2} 2^{1-q})
.
Edit:
est le plus petit flottant (en valeur absolue), et
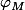
est le plus grand flottant.
par legeniedesalpages » 14 Nov 2007, 01:26
je vois pas la feinte pour la démo.
Je vois pas bien que
-x|\leq \frac{1}{2} 2^{q-1})
, mais après lorsqu'on divise par |x|, je vois pas.
par legeniedesalpages » 14 Nov 2007, 02:10
ah oui pardon, j'ai oublié de préciser que
est le plus petit flottant (en valeur absolue), et
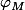
est le plus grand flottant.
:hum:
par legeniedesalpages » 14 Nov 2007, 02:15
Si
\setminus ]-1,1[)
:
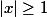
, donc
.
D'autre part
-x|\leq \frac{1}{2^q} = \frac{1}{2} 2^{q-1})
.
Donc
-x|}{|x|} \leq \frac{1}{2} 2^{q-1})
.
Reste le cas où
\cap ]-1,1[)
où j'ai du mal. :triste:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 71 invités
