Arithmethique polynôme

[mehdibj]

bonjours ,
on me demande de déterminer le pgcd de avec p et q premiers entre eux
je me suis pris de la manière suivante :


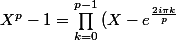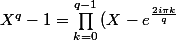je me suis dit que les facteurs en communs sont tels que avec k<p et k'<q
cas particuliers k=k' : k=0 (X-1) est un facteur en commun
cas 2 : k différent de k' : qk-pk'=0 ==>
n'est pas dans N cas p est premiers avec q et q est dans N d'où le seul facteur est (X-1)
j'ai conclu que
et sauf qu'avec ce resultat j'arrive à des contradictions donc je suis pas sur de ce dernier. où est ma faute ?
merci

[Ben314]

Salut,
Sur le principe, la méthode (décomposition dans C) est bonne (il y en aurait évidement d'autres), mais la rédaction déconne :

... n'est pas dans N cas p est premiers avec q et q est dans N...

là, autant le résultat est correct (i.e. à part pour k=k'=0, il n'y a pas d'autres racines commune), autant cette phrase me semble pas mal fausse (ou au minimum extrêmement mal dite). Même en la relisant 3 fois, je ne comprend pas pourquoi k'/k n'est pas dans N.

...j'ai conclu que
et sauf qu'avec ce resultat j'arrive à des contradictions donc je suis pas sur de ce dernier. où est ma faute ?

Si, c'est bien ça.
A mon avis, ça serait plus simple d'écrire que ppcm=(X^p-1)(X^q-1)/(X-1), mais si tu tient absolument à l'écrire sous forme de somme, pourquoi pas (ça a l'avantage de (re)montrer que (X^q-1)/(X-1) est bien un polynôme)

[mehdibj]

Même en la relisant 3 fois, je ne comprend pas pourquoi k'/k n'est pas dans N.

n'est pas dans N car p et q sont premiers entre eux : si est dans N cela voudrais dire que ce qui nous donne que p et q ne sont pas premiers entre eux (c'est le cas où )
mais bon si mon resultat est correcte je ne vois pas comment je pourrrais montrer que ( j'ai déjà montrer que divise et divise )

[Ben314]

Même en la relisant 3 fois, je ne comprend pas pourquoi k'/k n'est pas dans N.

n'est pas dans N car p et q sont premiers entre eux : si est dans N cela voudrais dire que ce qui nous donne que p et q ne sont pas premiers entre eux (c'est le cas où )

Effectivement (j'aurais du relire une 4em fois...)

je ne vois pas comment je pourrais montrer que divise ( j'ai déjà montré que divise et divise )

Le truc rouge est faux et celui en bleu est... pas très utile...
Sinon, via la question précédente, tu connait et tu peut en déduire la valeur de . Quelle sont ces racines ? Avec quel ordre du multiplicité ? Est-ce que ce sont des racines de ?

[mehdibj]

je ne vois pas comment je pourrais montrer que divise ( j'ai déjà montré que divise et divise )

Le truc rouge est faux et celui en bleu est... pas très utile...
Sinon, via la question précédente, tu connait et tu peut en déduire la valeur de . Quelle sont ces racines ? Avec quel ordre du multiplicité ? Est-ce que ce sont des racines de ?[/quote]
faute de frappe je voulais dire que divise et divise