Approximation de n!

[may prepa]

bonjours,
je souhaiterai que quelqu'un me dise si ce que j'ai fait est juste svp...la fonction qu'on donne est : Un= =ln(n!)-nln(n)+n-0.5ln(n)
J'ai montré que Un-U(n+1)=A/n^2 avec A constante réelle.
Pour en déduire que Un converge est ce que j'ai le droit de dire : Lim A/n^2=0 quand n-> infini, donc Un=U(n+1) quand n->infini, donc Un converge ,on note L sa limite?

Ensuite je dois montrer qu'il existe K réel tel que : n!~(K*n^n*n^(1/2))/exp(n).
Pour cela j'ai transformer légalité Un=... en ln(n!)=nln(n)-n+0.5ln(n)+Un, en passant à l'exponentielle j'obtient : n!=(n^n*n^0.5*exp(Un))/exp(n).
Et comme Lim Un = L quand n->infini lim exp(Un)=Exp(L)=K
D'ou l'égalité demandée.
Donc si quelqu'un pouvait me dire si mon raisonnement est juste svp?

[abcd22]

Bonjour,

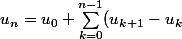J'ai montré que Un-U(n+1)=A/n^2 avec A constante réelle.
Pour en déduire que Un converge est ce que j'ai le droit de dire : Lim A/n^2=0 quand n-> infini, donc Un=U(n+1) quand n->infini, donc Un converge, on note L sa limite?

Non, on ne peut pas dire que Un=U(n+1) car c'est faux, même si la différence entre les deux tend vers zéro, une limite n'est pas une égalité, et il ne suffit pas d'avoir U(n+1) - Un qui tend vers 0 pour que Un converge (contre-exemple : ln(n)).
Par ailleurs, la première égalité que tu as écrite est une équivalence, une équivalence non plus n'est pas une égalité.
On a ...