Ben, déjà et pour commencer, il faut bien comprendre que ces deux symboles
ont un sens totalement différent et qu'il est extrêmement rare (dans les maths "usuelles") que l'on ait en même temps

et

.
Le symbole

il veut dire "appartient" : ce que tu met à gauche du symbole, c'est
un élément de l'ensemble qui est à droite du symbole.
Par exemple

, ou

ou

où M est un point et
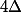
une droite (c'est à dire un ensemble de points).
Le symbole

il veut dire "est inclus dans" (ou "est contenu dans") : ce que tu met à gauche du symbole, c'est
un ensemble qui est
une partie de l'ensemble qui est à droite du symbole.
Par exemple

(et, de façon générale, écrire

, c'est la même chose que

) ou

ou

où [AB] est un segment et
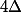
une droite (c'est à dire deux ensemble de points).
En math, on fait une grosse (voire une énooooorme) différence entre
l'élément x et
le singleton {x} qui est l'ensemble contenant un unique élément x.
Après, on peut s'amuser à écrire des trucs du style :

Enfin, vu que tu parle de l'ensemble des parties d'un ensemble A, on a effectivement (par définition) l'équivalence
)
.
Mais il faut bien voir que
)
c'est un ensemble un peu compliqué.
Si X={a,b,c}, saurait tu m'écrire

(X)={...} ?
Et pour revenir a tes trucs de départ,
-
)
ça veut dire que {a} est
un élément de P(A), c'est a dire
une partie de A, c'est à dire qu'en fait a est un élément de A.
Donc
\ \Leftrightarrow\ a\in A)
-
)
ça veut dire que {a} est
une partie de P(A), c'est à dire que a est
un élément de P(A), c'est a dire
une partie de A.
Donc
\ \Leftrightarrow\ a\in{\mathcal P}(A)\ \Leftrightarrow\ a\subset A)