Anneau Z[X]

par **rain** » 01 Fév 2009, 12:24

Bonjour, est-ce que quelqu'un pourrait m'expliquer pourquoi l'Anneau Z[X] est principal?
Je dirai que c'est parce que si P dans Z[X],
P(X)=a0+a1X+...+anX^n, et donc c'est une combinaison linéaire d'éléments de Z et de puissances de X, donc il est engendré par X. Est-ce que c'est çà?

par **ThSQ** » 01 Fév 2009, 12:46

rain a écrit:pourquoi l'Anneau Z[X] est principal?

Ca risque d'être dur de trouver quelqu'un ...

= ?????

par **skilveg** » 01 Fév 2009, 12:57

Je crois que le mieux que l'on puisse dire, c'est qu'il est factoriel et noethérien, tout ceci utilisant le fait que ces notions sont stables par passage à l'anneau de polynômes.

par **rain** » 01 Fév 2009, 13:08

skilveg a écrit:Je crois que le mieux que l'on puisse dire, c'est qu'il est factoriel et noethérien, tout ceci utilisant le fait que ces notions sont stables par passage à l'anneau de polynômes.

Pourquoi? C'est quoi la relation entre factoriel, noethérien et principal?(nothérien je trouve pas de définition claire, si tu pouvait m'en donner une, çà m'aiderai beaucoup).

par **skilveg** » 01 Fév 2009, 13:46

Principal implique noethérien et factoriel. Un anneau est noethérien si tous ses idéaux sont de type fini, ou si toute suite croissante d'idéaux stationne, ou si tout ensemble non vide d'idéaux admet un élément maximal (cf Perrin, cours d'algèbre).

par **ThSQ** » 01 Fév 2009, 14:04

rain a écrit:Pourquoi? C'est quoi la relation entre factoriel, noethérien et principal?(nothérien je trouve pas de définition claire, si tu pouvait m'en donner une, çà m'aiderai beaucoup).

Concentre toi sur la notion d'anneau principal déjà !

est ce que l'idéal (= polynômes entiers à coeff constant pair) est principal ?

par **rain** » 01 Fév 2009, 14:15

ThSQ a écrit:Concentre toi sur la notion d'anneau principal déjà !

est ce que l'idéal (= polynômes entiers à coeff constant pair) est principal ?

Je sais pas du tout, est principal s'il est engendré pas un seul élément, donc je dirai qu'il est engendré par X (mais pas sur de moi).

par **skilveg** » 01 Fév 2009, 14:17

Non. Si

était engendré par

, on devrait avoir, dans

,

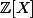
et

. Qu'est-ce qu'on en déduit?

par **rain** » 01 Fév 2009, 14:21

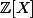
skilveg a écrit:Non. Si était engendré par , on devrait avoir, dans , et . Qu'est-ce qu'on en déduit?

deg(P(X))=0?

par **skilveg** » 01 Fév 2009, 14:32

Mais encore?

par **rain** » 01 Fév 2009, 14:34

;;;;P(x)=1

par **jeje56** » 01 Fév 2009, 14:36

Que <2,X> n'est pas principal (engendré par deux éléments, 2 et X)

par **jeje56** » 01 Fév 2009, 14:39

On a l'équivalence : A corps ssi A[X] principal
Or Z est-il un corps ?

par **rain** » 01 Fév 2009, 14:42

OK Z c'est pas un corps donc Z[X] est pas principal.Et si on prend K un corps, K[X] est principal, quelqu'un connait une démo de cette propriété?

par **skilveg** » 01 Fév 2009, 16:02

Si

est un corps,

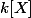
est euclidien, et en particulier principal.

par **ThSQ** » 01 Fév 2009, 18:22

jeje56 a écrit:Que n'est pas principal (engendré par deux éléments, 2 et X)

Et ne pas oublier de dire que != Z[X] pour conclure

par **skilveg** » 01 Fév 2009, 19:17

Une petite remarque: ce n'est pas parce qu'un idéal est engendré par deux éléments qu'il n'est pas principal (l'un des deux éléments peut très bien diviser l'autre). Là, on utilise le fait qu'un diviseur commun à 2 et X est nécessairement inversible.

Anneau Z[X]

Anneau Z[X]

Qui est en ligne