Soit A un anneau (pas forcement unitaire).
Quelque soit x appartenant à A, x^3=x et 2x=0.
Montrer que A est commutatif.
Et si c'est trop facile, il y a aussi la même chose avec 3x=0 à la place de 2x=0.
Sinon, il y a le cas general (sans 2x=0 ni 3x=0).
indic : à la première question il fallait montrer qu'avec x^3=x on a 6x=0.
A un anneau, x^3=x et 2x=0. Montrer que A commutatif
9 messages
- Page 1 sur 1
Shadok a écrit:Soit A un anneau (pas forcement unitaire).
Quelque soit x appartenant à A, x^3=x et 2x=0.
Montrer que A est commutatif.
Et si c'est trop facile, il y a aussi la même chose avec 3x=0 à la place de 2x=0.
Sinon, il y a le cas general (sans 2x=0 ni 3x=0).
indic : à la première question il fallait montrer qu'avec x^3=x on a 6x=0.
Donc
En effet les hypotheses 2x = 0 ou 3x = 0 ne sont pas du tout necessaires.
[EDIT] bonne question Kazeriahm: on se demande quand meme????
Bonjour,
c'est complétement faux ...
Déjà 0^3=0 et pourtant on n'a pas 0^2=1
Sinon prend par exemple une matrice A telle que A^3-A=0.
Une telle matrice serait donnée par n'importe quelle matrice ayant des 0 et des 1 sur sa diagonale ou toute matrice semblable à une matrice de ce type.
RadarX a écrit:[TEX]x^3 = x \,==>\, x^2 = 1
c'est complétement faux ...
Déjà 0^3=0 et pourtant on n'a pas 0^2=1
Sinon prend par exemple une matrice A telle que A^3-A=0.
Une telle matrice serait donnée par n'importe quelle matrice ayant des 0 et des 1 sur sa diagonale ou toute matrice semblable à une matrice de ce type.
RadarX : d'abord il est précisé que A n'est pas nécessairement unitaire.
Ensuite, pour passer de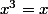 à
à 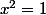 , il y a peut-être une difficulté...
, il y a peut-être une difficulté...
:marteau:
Voici une démo qui m'a l'air correcte, en revanche :
(1) Hypothèses : pour tout dans A,
dans A, 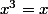 et
et 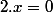 .
.
Soit un élément de A. On calcule
un élément de A. On calcule
^2=x^2+2x^3+x^4=0) donc
donc
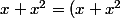^3=(x+x^2)\times 0=0)
et ainsi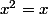 pour tout élément
pour tout élément  de A.
de A.
Donc pour tous et
et  dans A,
dans A,
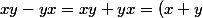^2-(x+y)=0) CQFD.
CQFD.
(2) Hypothèses : pour tout dans A,
dans A, 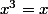 et
et 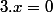 .
.
On se fixe deux éléments et
et  de A.
de A.
Alors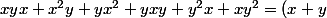^3-x^3-y^3=x+y-x-y=0)
et de même
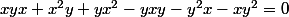 .
.
En faisant la somme, on trouve (en utilisant l'hypothèse de départ) :
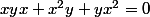 .
.
Multipliant à gauche par , on trouve
, on trouve
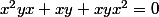 .
.
Multipliant à droite par , on trouve
, on trouve
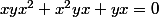 .
.
Par différence, on conclut que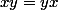
(3) Hypothèse : pour tout dans A,
dans A, 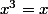 .
.
Pour tout élément de A, on a
de A, on a 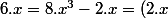^3-2.x=0)
Soient et
et  deux éléments quelconques de A.
deux éléments quelconques de A.
On remarque que=0=2.(3.x)) .
.
En adaptant le raisonnement (2), on trouve que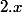
commute avec
(l'argument crucial est le fait que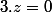 quel que soit
quel que soit 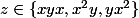 ).
).
En adaptant le raisonnement (1), on prouve facilement que
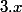 et
et 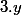 commutent
commutent
(remarquer que=2.(3.y)=2.(3.x+3.y)=0) ).
).
On a donc prouvé que=0) et
et =0) .
.
En combinant les deux, on trouve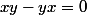 . CQFD.
. CQFD.
Ensuite, pour passer de
:marteau:
Voici une démo qui m'a l'air correcte, en revanche :
(1) Hypothèses : pour tout
Soit
et ainsi
Donc pour tous
(2) Hypothèses : pour tout
On se fixe deux éléments
Alors
et de même
En faisant la somme, on trouve (en utilisant l'hypothèse de départ) :
Multipliant à gauche par
Multipliant à droite par
Par différence, on conclut que
(3) Hypothèse : pour tout
Pour tout élément
Soient
On remarque que
En adaptant le raisonnement (2), on trouve que
commute avec
(l'argument crucial est le fait que
En adaptant le raisonnement (1), on prouve facilement que
(remarquer que
On a donc prouvé que
En combinant les deux, on trouve
Pour la troisième étape de mon raisonnement, on peut en fait s'appuyer
de façon plus directe sur les précédentes, en raisonnant comme suit :
on introduit les idéaux bilatères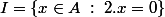
et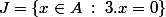 de l'anneau A.
de l'anneau A.
Le morphisme canonique
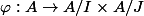 est alors injectif
est alors injectif
(si un élément x vérifie 3.x=0 et 2.x=0, alors x=0).
L'anneau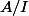 vérifie les hypothèses (1),
vérifie les hypothèses (1),
et l'anneau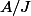 vérifie les hypothèses (2).
vérifie les hypothèses (2).
Ces deux anneaux sont donc commutatifs, et puisque A est isomorphe à un sous-anneau de leur produit, il est lui-même commutatif.
En fait, A est même isomorphe à l'anneau produit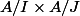 .
.
En effet, si on prend deux éléments et
et  de A,
de A,
l'élément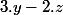 est congru à
est congru à  modulo
modulo 
et à modulo
modulo  , ce qui assure que
, ce qui assure que 
est surjective.
de façon plus directe sur les précédentes, en raisonnant comme suit :
on introduit les idéaux bilatères
et
Le morphisme canonique
(si un élément x vérifie 3.x=0 et 2.x=0, alors x=0).
L'anneau
et l'anneau
Ces deux anneaux sont donc commutatifs, et puisque A est isomorphe à un sous-anneau de leur produit, il est lui-même commutatif.
En fait, A est même isomorphe à l'anneau produit
En effet, si on prend deux éléments
l'élément
et à
est surjective.
Vedeus a écrit:RadarX : d'abord il est précisé que A n'est pas nécessairement unitaire.
Ensuite, pour passer deà
, il y a peut-être une difficulté...
:marteau:
Voici une démo qui m'a l'air correcte, en revanche :
(1) Hypothèses : pour toutdans A,
et
.
Soitun élément de A. On calcule
donc
et ainsipour tout élément
de A.
Donc pour touset
dans A,
CQFD.
(2) Hypothèses : pour toutdans A,
et
.
On se fixe deux élémentset
de A.
Alors
et de même.
En faisant la somme, on trouve (en utilisant l'hypothèse de départ) :.
Multipliant à gauche par, on trouve
.
Multipliant à droite par, on trouve
.
Par différence, on conclut que
(3) Hypothèse : pour toutdans A,
.
Pour tout élémentde A, on a
Soientet
deux éléments quelconques de A.
On remarque que.
En adaptant le raisonnement (2), on trouve que
commute avec
(l'argument crucial est le fait quequel que soit
).
En adaptant le raisonnement (1), on prouve facilement queet
commutent
(remarquer que).
On a donc prouvé queet
.
En combinant les deux, on trouve. CQFD.
Merci beaucoup. Et pour repondre à ceux d'en haut c'était de l'aide qui était demandée. :we:
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
