Anneau non factoriel
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
brouversliet
- Membre Naturel
- Messages: 12
- Enregistré le: 23 Oct 2019, 13:41
-
 par brouversliet » 31 Oct 2019, 15:11
par brouversliet » 31 Oct 2019, 15:11
Bonjour,
Je cherche à montrer que l'anneau

n'est pas factoriel.
Pour cela, on introduit
=a^2+5b^2)
, on montre que
=N(\alpha) N(\beta))
et que

est inversible dans

si et seulement si
=1)
.
On considère ensuite
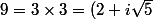 \times (2-i \sqrt{5}))
et on montre que

,

et

sont irréductibles (en utilisant

).
On obtient donc deux décompositions en irréductibles distinctes. Cependant, dans la définition d'anneau factoriel, on dit que la décomposition est unique "à inversible près". Je ne vois pas trop ce que signifie "réellement" cette condition et comment l'appliquer "concrètement" dans ce cas précis.
En clair, comment justifier proprement que ces deux décompositions sont bien distinctes et non "égales
modulo inversible" ?
Merci d'avance !
-
GaBuZoMeu
- Habitué(e)
- Messages: 6140
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 31 Oct 2019, 15:19
par GaBuZoMeu » 31 Oct 2019, 15:19
L'élément

du corps de fractions

n'appartient pas à

: l'élément irréductible

n'est pas associé à l'élément irreductible

, l'un n'est pas le produit de l'autre par un inversible de

.

-
jsvdb
- Membre Naturel
- Messages: 89
- Enregistré le: 20 Jan 2017, 09:45
-
 par jsvdb » 31 Oct 2019, 15:23
par jsvdb » 31 Oct 2019, 15:23
Bonjour
brouversliet.
La question à te poser est : " est-ce que

est associé à

ou à

".
Si la réponse est non, c'est que 9 admet bien deux décomposition distinctes non associables.
Par exemple, dans
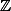
, 9 admet deux décompositions qui sont 3*3 et (-3)*(-3).
Les inversibles de
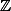
sont 1 et -1.
Donc les deux seules décompositions de 9 dans
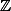
sont "fabriquées" avec des éléments associés.
Bienheureux les fêlés car ils laissent passer la lumière !
-
brouversliet
- Membre Naturel
- Messages: 12
- Enregistré le: 23 Oct 2019, 13:41
-
 par brouversliet » 31 Oct 2019, 15:26
par brouversliet » 31 Oct 2019, 15:26
Ok, merci !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
