Anneau intègre et fini => corps

[Cryptocatron-11]

Bonsoir ,

Je souhaite démontrer que "Tout anneau intègre fini est un corps ".

J'ai bien compris qu'il fallait prendre un élément a non nul de l'anneau A et montrer qu'il est inversible (par définition du corps).

J'ai lu quelque part que
dans un anneau A intègre, pour a non nul, l'application qui à x associe ax est injective. Cette condition suffit à assurer que tout élément non nul possède un inverse pour la multiplication si l'anneau A est fini (l'application b ab étant alors bijective, l'antécédent de 1 est l'inverse de a), mais pas dans le cas général.

déjà ce que je comprend pas, c'est pourquoi ils disent pas directement que l’application x ax est bijective ?

Puis aussi , j'ai lu que si c'est bijectif alors on peut trouver un b tel que f(b)=1 (1 étant l'élément neutre de *) et dans ce cas, f(b) = 1 = a*b, ce qui prouve que a est inversible
Très franchement je vois pas comment ils arrivent à trouver ce 1
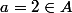
Exemple (pour illustrer mes propos) avec l'anneau (Z,+,*) : On prend . Soit f:=x ax. Comment peuvent ils dirent qu'ils existent un b tel que f(b)=1 ? Si on prend a = 2, que vaut b , je serais très curieux de le savoir !!!

[Skullkid]

Bonsoir, une application injective entre deux ensembles finis de même cardinal est bijective (c'est une propriété très importante). Ensuite, comme ton application f est bijective, 1 a un antécédent, qu'ils appellent b.

Ton contre-exemple n'en est pas un puisque Z n'est pas un anneau fini, aux dernières nouvelles. D'ailleurs, l'application n -> 2n n'est pas bijective de Z dans Z.

[Clu]

Pour montrer qu'elle est injective,
Si tu considères l'application f: x->a*x qui va de A dans A (où A est l'anneau considéré et a est un élément non nul de A) alors f est un morphisme de groupe (du groupe A).
En outre le noyau de f est nul (car A est intègre) donc (théorème du cours) f est injective

[Cryptocatron-11]

Ensuite, comme ton application f est bijective, 1 a un antécédent, qu'ils appellent b.

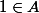
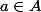
Oui mais ça suppose que et ça j'ai l'impression que ça sort d'un chapeau magique. Puis d'après ce qu'a dit Clu , (vu que c'est le neutre pour *) et et on doit forcément avoir 1=b.a mais ce b , c'est pas forcé qu'il appartienne à A ...

[Skullkid]

C'est quoi ta définition de "bijective" ?

[Cryptocatron-11]

si f est injective et surjective alors c'est bijectif , mathématiquement ça se traduit par

[Skullkid]

Et ici c'est qui F ?

[Cryptocatron-11]

ben F c'est A en fait

[Skullkid]

Oui, donc puisque f est bijective, 1, qui est un élément de A, a un (unique) antécédent noté b, qui est lui aussi dans A.

[Cryptocatron-11]

En plus quand j'ai dit que F c'est A , c'était supposé que F est inclu dans A et comme c'est bijectif donc F=A
Sauf que justement pourquoi F est inclu dans A ? Si je multiplie tous les éléments de A par machin et comme A est fini et bien je vais retrouver des éléments qui n'appartiennent plus à A :triste:
Est ce parce c'est stable pour * ?

[Skullkid]

La définition d'une loi de composition interne sur A c'est une application de A² dans A. Donc non, tu ne peux pas sortir de A en multipliant des objets de A entre eux, de la même façon qu'en multipliant deux entiers entre eux, tu ne tomberas jamais sur une matrice. Le fait que A soit fini ou pas n'a rien à voir ici.

[Cryptocatron-11]

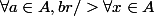
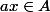
Oui j'avais du mal à cause du fait que A soit fini mais là je comprends mieux car par définition , vu que * est interne

Merci

[Sylviel]

Dans la définition actuelle de corps il y a la commutativité... Et l'assertion 'tout anneau intègre fini est un corps' reste vraie. Mais la démonstration est autrement plus compliquée (Théorème de Wedderburn).

[Skullkid]

Dans la définition actuelle de corps il y a la commutativité...

Salut, cette définition actuelle date de quand ? En ce qui me concerne on m'a appris qu'il y avait ambiguïté (en français du moins) quand on parlait de corps, de la même façon que la définition d'un anneau peut inclure ou pas la présence d'un neutre multiplicatif.

[Sylviel]

Je ne saurais pas citer précisément de date, mais je sais que les programmes de prépas, et ceux de l'agreg si je ne m'abuses, ont choisit de retenir pour corps la commutativité (choix dommageable à mon humble avis), et pour anneaux la présence d'un neutre (choix moins dommageable ? --> il suffit de parler d'idéal).

P.S : je ne pense pas qu'ici la commutativité soit attendue, je voulais juste donner ce résultat plutot sympa.

[JackeOLanterne]

Un corps gauche est aussi un anneau à division (skew field en V.O) dont le représentant le plus connu s'appelle H (quaternions). La théorie de Galois applicable aux corps commutatifs se généralise à leurs cas. En outre, les extensions de corps interviennent en géométrie. Les portes s'ouvrent vers de la ramification.