Anneau Z/pZ avec p premier

[Hao]

Bonsoir,

J'ai une question sur un exercice qui me pose des problèmes:

Le but de cet exercice est de démontrer que tout nombre premier p>=2 divise (p-1)!+1.

Quels sont les éléments inversibles de Z/pZ égaux à leur inverse?
En déduire:
dans Z/pZ: (p-1)!=-1.

Voila, les éléments inversibles de Z/pZ sont tous les éléments qui sont premier avec p, mais comment est ce qu'on peut trouver les éléments inversibles de Z/pZ égaux à leur inverse?

Et je n'arrive pas à une déduction de: (p-1)!=-1 dans Z/pZ

Merci d'avance

[abcd22]

Bonsoir,
Un élément x non nul (Z/pZ est un corps) de Z/pZ est égal à son inverse si et seulement si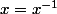 par définition. Yapluka résoudre.
(p;););)1)! = 1 × 2 × 3 × … × (p;););)1), ce sont tous les éléments non nuls de Z/pZ, on les groupe en deux catégories : ceux qui sont égaux à leur inverse et les autres (qui ont un inverse qui est dans le produit…).

[leon1789]

hé l'eau :id:

Si on travaillait dans R (par exemple), comment ferais-tu pour connaître les éléments égaux à leur propre inverse ?

EDIT : arf grilled I'm

[ThSQ]

Décidément Wilson est à l'honneur aujourd'hui !

[leon1789]

Décidément Wilson est à l'honneur aujourd'hui !

:zen: tu l'as vu où aussi ?