Bonjour à tous .
Je rencontre des difficultés pour les 3 questions qui vont suivre , merci de votre aide par avance !
Dans l'exercice voici les données :
On a une application linéaire R^2 -> R^3 définie par h (x et y en dessous )= ( 3x + y)
(3y +x )
(3y + 3x)
Soit f l'application linéaire pour laquelle v1 = (3, puis 1 en dessous) est un vecteur propre de valeur propre 1 et v2 = (2, puis en dessous 1) est un vecteur propre de valeur propre -1.
1) Écrire le vecteur w = f (2, puis en dessous 5 )
2)Écrire la matrice qui représente f par rapport à la base canonique de R^2 ( pour cette question j'ai 2 pistes: j'hésite soit a écrire la matrice f composé de 3,2 puis en dessous 1,1 ou alors remplacer les vecteur propre dans la matrice h , je suis perdue :/ )
3)L'application linéaire f est-elle diagonalisable ? ( pour ceci je sais qu'une application linéaire A : B -> B est diagonalisable s'il existe une base B' de B formée des vecteurs propres de A ) mais je vois pas comment faire :/
Algèbre linéaire : application linéaire
9 messages
- Page 1 sur 1
Salut. Tu peux essayer d'écrire (3;5) comme combinaison linéaire de v1 et v2, et comme tu connais f(v1) et f(v2) tu trouves.
Par contre otes moi d'un doute. Tu n'aurais pas recopier les questoins dans un ordre aléatoire? Car ton exo a bcp plus de sens quand tu commences par la 3e, puis la 2e, puis la 1ere.
La 3e, effectivement ya juste a regarder l'écnoné: (v1,v2) est une base de vecteur propre, qui donne ensuite la 2e si tu connais les formules d'écriture d'application linéaire en changeant de base,
et la 1ere en découle une fois que tu connais la matrice de f dans la base canonique...
Par contre otes moi d'un doute. Tu n'aurais pas recopier les questoins dans un ordre aléatoire? Car ton exo a bcp plus de sens quand tu commences par la 3e, puis la 2e, puis la 1ere.
La 3e, effectivement ya juste a regarder l'écnoné: (v1,v2) est une base de vecteur propre, qui donne ensuite la 2e si tu connais les formules d'écriture d'application linéaire en changeant de base,
et la 1ere en découle une fois que tu connais la matrice de f dans la base canonique...
Ok c'est bizarre. je sais pas quoi te dire, je te proposerai bien de faire lexo en le prenant par la fin car je comprends pas du tout la logique des questions.
pour la 3) donc on est d'accord que tu travailles sur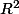 , donc un espace de dimension 2, et que par définition, v1 et v2 sont 2 vecteurs propres non colinéaires de f? ca conclut quasiment la question.
, donc un espace de dimension 2, et que par définition, v1 et v2 sont 2 vecteurs propres non colinéaires de f? ca conclut quasiment la question.
ensuite pour la 2) si tu connais la matrice d'une application linéaire dans une base (ici v1, v2),et que tu connais la matrice de passage de la base canonique dans (v1,v2) alors sais tu écrire la matrice de cette application linéaire dans la base canonique?
pour la 3) donc on est d'accord que tu travailles sur
ensuite pour la 2) si tu connais la matrice d'une application linéaire dans une base (ici v1, v2),et que tu connais la matrice de passage de la base canonique dans (v1,v2) alors sais tu écrire la matrice de cette application linéaire dans la base canonique?
MouLou a écrit:Ok c'est bizarre. je sais pas quoi te dire, je te proposerai bien de faire lexo en le prenant par la fin car je comprends pas du tout la logique des questions.
pour la 3) donc on est d'accord que tu travailles sur, donc un espace de dimension 2, et que par définition, v1 et v2 sont 2 vecteurs propres non colinéaires de f? ca conclut quasiment la question.
ensuite pour la 2) si tu connais la matrice d'une application linéaire dans une base (ici v1, v2),et que tu connais la matrice de passage de la base canonique dans (v1,v2) alors sais tu écrire la matrice de cette application linéaire dans la base canonique?
Merci pour ton aide ! oui ah je vois pour la 3!! et la 2 je t'ai mis ce que je pensais du moins j'ai ressortie ma définition et je l'ai appliquée
non c'est pas ca, je vois pas d'ou tu tire ce resultat? la matrice P=(3 2; 2 1) (2 en desosus de 3, 1 en dessous de 1). est la matrice des coordonnées de (v1,v2) dans la base canonique.
D=(1 0) est la matrice de f dans la base (v1,v2). Alors la matrice M de f dans la base canonique est
(0 -1) égale a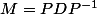 . je te laisse inverser P et finire le calcul.
. je te laisse inverser P et finire le calcul.
Sinon une méthode qui revient exactement au même, qui consiste à chercher à exprimer (1,0) et (0,1) dans la base (v1,v2), cad les écrire comme combinaison linéaire de v1 et v2, et connaissant f(v1), f(v2) tu sais calculer f((1,0)) et f((0,1)), et ca te donne sa matrice dans la base canonique.
Mais quand t'y réfléchis, exprimer (1,0) et (0,1) en fonction de v1 et v2 revient exactement à inverser P. c'est pour ça que ca revient au même, mais cette méthode permet de mieux visualiser le truc à mon sens.
D=(1 0) est la matrice de f dans la base (v1,v2). Alors la matrice M de f dans la base canonique est
(0 -1) égale a
Sinon une méthode qui revient exactement au même, qui consiste à chercher à exprimer (1,0) et (0,1) dans la base (v1,v2), cad les écrire comme combinaison linéaire de v1 et v2, et connaissant f(v1), f(v2) tu sais calculer f((1,0)) et f((0,1)), et ca te donne sa matrice dans la base canonique.
Mais quand t'y réfléchis, exprimer (1,0) et (0,1) en fonction de v1 et v2 revient exactement à inverser P. c'est pour ça que ca revient au même, mais cette méthode permet de mieux visualiser le truc à mon sens.
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
