Aire d'une surface dans R^2

[ariel60]

Bonjour,
Voici mon problème...:
Soit (C)une courbe dans R^2 entourant une surface (S)
Montrer que l'aire de (S)=
En déduire l'aire de l'ellipse
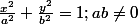
Pouvez-vous m'indiquer comment faire je vous en supplie...
Merci infiniment

[aviateur]

Bonjour
Soit A cette intégrale
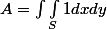
Par application simple du théorème de Green-Riemann on trouve que . Tu as ainsi la réponse à la première question.
Pour le calcul de A , une paramétrisation bien connue de l'ellipse est :
Il suffit d'utiliser ce paramétrage et alors le calcul de A est facile.

[chan79]

salut
Applique la formule de Green-Riemann avec P(x,y)=-y et Q(x,y)=x
:grillé

[ariel60]

Mais alors je ne comprends pas pourquoi avec le théorème Q'x-P'y,on n'obtient pas 0,la courbe n'est donc pas fermée??
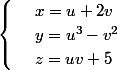
Et que faire si on donne le paramétrage de (S):je ne vois pas comment obtenir le résultat avec le (1/2)..

[aviateur]

Multi-post - multi forum, c'est terminé l'aide pour moi
https://www.ilemaths.net/sujet-aire-d-une-surface-771313.html

[ariel60]

Bonjour,
Je m'excuse vraiment pour le multi post mais j'aurai vraiment besoin votre aide..
Merci infiniment

[aviateur]

Bon

Mais alors je ne comprends pas pourquoi avec le théorème Q'x-P'y,on n'obtient pas 0,la courbe n'est donc pas fermée??

Je ne vois pas le rapport, tu dois confondre avec autre chose.

Pour le premier exercice
1. as-tu appliqué le théorème de Green-Riemann, qu'est ce que cela donne?

2. pour le calcul as-tu utiliser le paramétrage?

Pour le deuxième exercice (de tout façon la répons e c'est l'infini mais ...)
Peux tu donner le calcul de M'(u) et de M'(v)? ensuite on verra

[ariel60]

Bonjour,
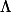
M'(u)=(1,2u,v);M'(v)=(2,-2v,u) ,M'(u)M'(v)=(2 u^2 + 2 v^2;2v-u;-2v-4u) ;la norme donne un truc très long puissance 1/2 donc je ne sais pas trop et pour le domaine c'est R^2 donc je ne vois comment intégrer..
Cordialement

[aviateur]

Il y a une erreur à M'(u) c'est 3u^2. De toute façon il faut abandonner cet exercice car si (u,v)\in R^2 le résultat c'est évidemment l'infini, l'intégrale est non convergente. Si on remplace R^2 par un domaine borné (il me semble) que seul un calcul numérique est possible.