Aire d'une surface
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 07 Avr 2013, 16:52
par egan » 07 Avr 2013, 16:52
Salut tout le monde,
Je me donne une surface définie par z = f(x;y) où f est un fonction C1 définie sur un ouvert U de R2.
Est-ce que vous êtes d'accord pour dire que l'aire de cette surface est donnée par:
^2} \sqrt{1+\frac{\partial f}{\partial y}(x;y)^2} dxdy)
Merci d'avance.
@+ Boris.
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 07 Avr 2013, 17:16
par adrien69 » 07 Avr 2013, 17:16
egan a écrit:Salut tout le monde,
Je me donne une surface définie par z = f(x;y) où f est un fonction C1 définie sur un ouvert U de R2.
Est-ce que vous êtes d'accord pour dire que l'aire de cette surface est donnée par:
^2} \sqrt{1+\frac{\partial f}{\partial y}(x;y)^2} dxdy)
Merci d'avance.
@+ Boris.
Salut, c'est pas ce que je connais comme formule.
Pour moi ce serait plutôt
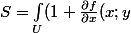^2 + \frac{\partial f}{\partial y}(x;y)^2 )^{\frac{1}{2}}dxdy)
-
egan
- Membre Rationnel
- Messages: 668
- Enregistré le: 03 Juil 2009, 15:32
-
 par egan » 07 Avr 2013, 17:36
par egan » 07 Avr 2013, 17:36
Comment tu justifies ça à la physicienne ?
Par contre pour une longueur de courbe, ça c'est bon non ?
^2} dx)
-
adrien69
- Membre Irrationnel
- Messages: 1899
- Enregistré le: 20 Déc 2012, 12:14
-
 par adrien69 » 07 Avr 2013, 19:16
par adrien69 » 07 Avr 2013, 19:16
Ouep pour la seconde.
Pour ce qui est de la physicienne, tu cherches en gros un carré transformé par la déformation que tu fais subir au plan : au premier ordre tu cherches la surface donnée par le parallélogramme formé par tes dérivées selon y et selon x. Et ça c'est la norme de leur produit vectoriel donc tu as le résultat. Du moins je crois.
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 08 Avr 2013, 10:58
par arnaud32 » 08 Avr 2013, 10:58
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
^2} \sqrt{1+\frac{\partial f}{\partial y}(x;y)^2} dxdy)