Aire d'un cylindre coupé par un autre
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 22 Jan 2012, 22:10
par Cryptocatron-11 » 22 Jan 2012, 22:10
Re bonsouuèère ,
Encore un problème d'analyse vectorielle ,
Calculer l'aire de la partie du cylindre C1:={(x,y,z)
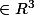
: x²+y²=R²} découpé par le cylindre C2:={(x,y,z)
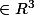
: x²+z²=R²}
Je vois comment ce que ça fait géométriquement : ce que j'ai donc pensé c'est dabord calculer l'aire totale du cylindre C1:={(x,y,z)
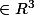
: x²+y²=R²}
Puis après lui retrancher la deux disques en forme de Pringles (comme les chips pringles :lol5: ) qui sont du au cylindre C2 qui le coupe
Mais je vois pas comment calculer la surface de ces deux pringles :triste:
merci pour votre aide
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 23 Jan 2012, 09:52
par Maxmau » 23 Jan 2012, 09:52
Cryptocatron-11 a écrit:Re bonsouuèère ,
Encore un problème d'analyse vectorielle ,
Calculer l'aire de la partie du cylindre C1:={(x,y,z)
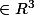
: x²+y²=R²} découpé par le cylindre C2:={(x,y,z)
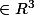
: x²+z²=R²}
Je vois comment ce que ça fait géométriquement : ce que j'ai donc pensé c'est dabord calculer l'aire totale du cylindre C1:={(x,y,z)
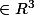
: x²+y²=R²}
Puis après lui retrancher la deux disques en forme de Pringles (comme les chips pringles :lol5: ) qui sont du au cylindre C2 qui le coupe
Mais je vois pas comment calculer la surface de ces deux pringles :triste:
merci pour votre aide
Bj
paramètre le cylindre C1 (coor cylindriques: x = Rcost , y = Rsint , z = u)
puis la partie intérieure au cylindre C2 ( simplement une des 2 chips, celle située du côté des y positifs par exemple ou même une demi chip)
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 23 Jan 2012, 10:35
par Cryptocatron-11 » 23 Jan 2012, 10:35
Maxmau a écrit:Bj
paramètre le cylindre C1 (coor cylindriques: x = Rcost , y = Rsint , z = u)
puis la partie intérieure au cylindre C2 ( simplement une des 2 chips, celle située du côté des y positifs par exemple ou même une demi chip)
Pour le chips du coté des y positif , je sais que z varie en -R et R.
et que x varie entre -R et R et y varie entre 0 et R.
Le problème c'est que dans l'ensemble x,y,z que je viens de cité ça marche pour une chips en forme de carré.
Il faudrait agir sur l'angle t mais je vois pas trop ...
En fait il faut que je m'arrange pour remonter l'axe z en faisant un rond avec l'angle t mais dur dur .
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 23 Jan 2012, 11:09
par Maxmau » 23 Jan 2012, 11:09
Cryptocatron-11 a écrit:Pour le chips du coté des y positif , je sais que z varie en -R et R.
et que x varie entre -R et R et y varie entre 0 et R.
Le problème c'est que dans l'ensemble x,y,z que je viens de cité ça marche pour une chips en forme de carré.
Il faudrait agir sur l'angle t mais je vois pas trop ...
En fait il faut que je m'arrange pour remonter l'axe z en faisant un rond avec l'angle t mais dur dur .
le point M(t,u) = ( Rcost , Rsint , u) décrit C1
Ce point M est à l'intérieur de C2 ss R²cos²t + u² < R² cad u² < R²sin²t
Donc la chip du côté des y positifs est décrite par M(t,u) pour 0<t<pi , -Rsint<u<Rsint
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 23 Jan 2012, 11:39
par Cryptocatron-11 » 23 Jan 2012, 11:39
Maxmau a écrit:le point M(t,u) = ( Rcost , Rsint , u) décrit C1
Ce point M est à l'intérieur de C2 ss R²cos²t + u² < R² cad u² < R²sin²t
Donc la chip du côté des y positifs est décrite par M(t,u) pour 0<t<pi , -Rsint<u<Rsint
Si ça aurait été coupé par un cylindre C3 (x,y,z) tel que

, On aurait fait

d'ou
<z<Rcos( \theta ))
et

?
En revenant à l'exo , l'idée c'est deux calculer cette aire du chips ensuite la multiplier par deux et la retrancher à l'aire du cylindre , c'est ça ?
Sinon pour l'aire du pringles j'ai trouvé
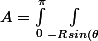}^{Rsin( \theta )} R dzd \theta =4R^2)
sauf erreur
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 23 Jan 2012, 12:32
par Maxmau » 23 Jan 2012, 12:32
Cryptocatron-11 a écrit:Si ça aurait été coupé par un cylindre C3 (x,y,z) tel que

, On aurait fait

d'ou
<z<Rcos( \theta ))
et

?
En revenant à l'exo , l'idée c'est deux calculer cette aire du chips ensuite la multiplier par deux et la retrancher à l'aire du cylindre , c'est ça ?
Sinon pour l'aire du pringles j'ai trouvé
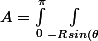}^{Rsin( \theta )} R dzd \theta =4R^2)
sauf erreur
pour l'aire trouvée je pense que c'est exact et que t'as répondu à la question posée
pour ta remarque "En revenant à l'exo , l'idée c'est deux calculer cette aire du chips ensuite la multiplier par deux et la retrancher à l'aire du cylindre , c'est ça ?" Alors là je suis perplexe
-
Cryptocatron-11
- Membre Rationnel
- Messages: 604
- Enregistré le: 18 Déc 2010, 20:19
-
 par Cryptocatron-11 » 23 Jan 2012, 13:04
par Cryptocatron-11 » 23 Jan 2012, 13:04
Maxmau a écrit:pour l'aire trouvée je pense que c'est exact et que t'as répondu à la question posée
pour ta remarque Alors là je suis perplexe
Oui c'est vrai qu'on cherche la partie découpé. Tu as raison. Au début j'avais dans l'idée de calculer l'aire du cylindre sans les deux chips, c'est pour ça.
Merci bcp pour ton aide . Si jamais t'as du temps , j'ai pas eu de réponse sur ce problème
là :lol3:
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 23 Jan 2012, 13:37
par Maxmau » 23 Jan 2012, 13:37
Cryptocatron-11 a écrit:Oui c'est vrai qu'on cherche la partie découpé. Tu as raison. Au début j'avais dans l'idée de calculer l'aire du cylindre sans les deux chips, c'est pour ça.
Merci bcp pour ton aide . Si jamais t'as du temps , j'ai pas eu de réponse sur ce problème
là :lol3:
si on cherche l'aire de la partie de C1 découpée par C2, c'est 2 chips
si on cherche la surface du solide intersection des 2 cylindres pleins, c'est 4 chips (2 sur C1 et 2 sur C2)
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 23 Jan 2012, 16:19
par Pythales » 23 Jan 2012, 16:19
La résolution de
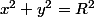
et

donne

c.a.d. que, du côté

le cylindre
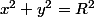
est coupé par le plan

.
La surface vaut donc la moitié de celle d'un quart de cylindre de base
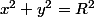
et de hauteur

-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 24 Jan 2012, 09:45
par Maxmau » 24 Jan 2012, 09:45
Pythales a écrit:La résolution de
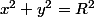
et

donne

c.a.d. que, du côté

le cylindre
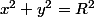
est coupé par le plan

.
La surface vaut donc la moitié de celle d'un quart de cylindre de base
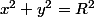
et de hauteur

Bj
Je comprends mal et puis ça ne me parait pas conforme au précédent résultat
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 24 Jan 2012, 12:55
par Maxmau » 24 Jan 2012, 12:55
Quel est alors le résultat ? il y a un facteur pi qui n'a pas lieu d'être ( à mon avis)
L'aire de toute la surface (du solide intersection des 2 cylindres pleins) est 16R²
-
Mathusalem
- Membre Irrationnel
- Messages: 1837
- Enregistré le: 14 Sep 2008, 03:41
-
 par Mathusalem » 24 Jan 2012, 15:49
par Mathusalem » 24 Jan 2012, 15:49
Maxmau a écrit:Quel est alors le résultat ? il y a un facteur pi qui n'a pas lieu d'être ( à mon avis)
L'aire de toute la surface (du solide intersection des 2 cylindres pleins) est 16R²
J'ai pas checké vos calculs, mais géométriquement je dirais que c'est 2 pi R^2
-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 24 Jan 2012, 16:12
par Maxmau » 24 Jan 2012, 16:12
Mathusalem a écrit:J'ai pas checké vos calculs, mais géométriquement je dirais que c'est 2 pi R^2
Désolé mais je ne suis pas du tout d'accord.
La méthode de Pythalès doit conduire à 4 pi R² (surface totale) et je ne suis pas non plus d'accord.
le plan y=z ne partage pas le quart de cylindre en 2 surfaces de même aire
-
Mathusalem
- Membre Irrationnel
- Messages: 1837
- Enregistré le: 14 Sep 2008, 03:41
-
 par Mathusalem » 24 Jan 2012, 16:44
par Mathusalem » 24 Jan 2012, 16:44
Maxmau a écrit:Désolé mais je ne suis pas du tout d'accord.
La méthode de Pythalès doit conduire à 4 pi R² (surface totale) et je ne suis pas non plus d'accord.
le plan y=z ne partage pas le quart de cylindre en 2 surfaces de même aire
Oui j'avais édité ma réponse mais apparemment ma connection internet a été bouffée.
J'avais dit que j'avais fini par poser le calcul, qu'effectivement le plan de coupe ne partage pas l'aire de la section circulaire en deux parts égales, et qu'en effet lorque l'on pose le calcul proprement, il sort 16R^2
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
