Forum de Mathématiques: Maths-Forum

C'est simplement un exo de khôlle sur les groupes.

Bonjour,

Comment puis-je montrer que (N, +) est un monoide commutatif ? Il faut juste que je dise que + est associative, commutative et que le neutre est 0 ? Mais donc on admet que + vérifie ces propriétés alors, cela découle de Peano non ? Merci

bonjour, Soit (u_n) telle que u_n=f(n). Je souhaite montrer qu'à partir d'un certain rang N, une suite u_n est strictement positive. Ce que j'ai fait, c'est que j'ai trouvé un entier N strictement positif pour lequel u_N >0. Puis, pour s'assurer que tous les entiers n>=N, u_n>0, j'ai montré que l'in...

Ok je comprends mieux merci

tout partie non vide et majorée de R admet une borne supérieure. Pourtant cet ensemble est bien une partie de R non vide, borné donc majoré. Pourquoi n'admet-elle pas de borne sup d'après le théorème.

Bonjour,

Je voulais savoir pourquoi la partie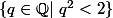 n'est pas une partie de . Merci.

Ok je suis d'accord.

Si vous obtenez u_n+1 en fonction de u_n et de n, il sera plus difficile de calculer u_24 par exemple. Il faudra calculer tous les u_n pour n inférieur à 24. Sauf si on tombe sur une suite classique.

Ok je suis d'accord. Je pensais que la formule de un+1 en fonction de u_n et de n n'était que de l'ordre de la conjecture et qu'il fallait encore la redemontrer par reccurence. Pourquoi donc on montre une formule par reccurence et pas l'autre sachant que pour la première on aurait pu dire que de man...

Bah oui évidemment. Cela revient en fait à déterminer l'expression de (u_n) par récurrence donc u_n+1 en fonction de u_n. Mais ce que je me dis c'est est-ce qu'on trouve cette formule, on l'utilise dans l'hérédité et c'est OK, ou est ce qu'on conjecture cette formule, on la démontre par reccurence a...

Si je connais parfaitement le principe de reccurence, simple, double forte. Ce que je dis c'est que la formule conjecturee doit être montrée par reccurence non ?. Pour l'hérédité, comment on s'y prendrai ? On part de u_n+1 mais ensuite ?

Bonjour, Vous connaissez sans doute l'exo du château de cartes où il faut trouver une formule générale pour le nombre de cartes en fonction du nombre d'étages. Soit (u_n) la suite donnant le nombre de cartes et n le nombre d'étages. J'ai conjecturé u_n=(n(3n+1))/2 en calculant le nombre de cartes po...