Forum de Mathématiques: Maths-Forum

Bonsoir, http://img15.hostingpics.net/pics/823422tore.jpg Je sais que l'homologie H_1 du tore à deux trous est \mathbb{Z}^4 où les quatre générateurs sont les courbes rouges et bleues claires. Je me demande quelle est la classe des deux courbes verte et violette dans l'homologie.. Avez-vous une idée...

Parfait, c'est clair. Merci beaucoup

Bonsoir, je suis à la recherche de la présentation (en terme de générateurs et relations) du groupe affine, définit comme étant l'ensemble des matrices \begin{pmatrix} a & b \\ \\ 0 & 1 \end{pmatrix} avec a \in \left\{\pm 1\right} et b \in \mathbb{Z} Alors évidemment la présentation existe t...

Merci beaucoup cela m'aide, j'avance.

Bon..

Soit un -ev de dim finie .

On pose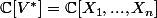

Voir : http://loic.foissy.free.fr/pageperso/cours3.pdf page 13 corollaire 17

Oui bon laissons tomber ces histoires d'indéterminées..

POSONS

Ca va comme définition ?

Je comprends pas trop ton problème.. Pour V^* chaque élément se décompose via la base des e_i^* , donc il y a n indéterminées e_1^*,...,e_n^* . Si tu comprends bien ce qu'est \mathbb{C}[W] avec W un ev de dim finie n , alors considère cet objet, puis imagine que en fait W=V^* , qui est bien un ev de...

Bah c'est pareil non ? Tu considères

(et puis en dim finie on a )

Supposons V de dimension finie tu as raison. Et aussi prenons V un \mathbb{C} -ev (cela fait coïncider les multiplications scalaires non ?) Je comprends pas pourquoi tu dis que la dimension de \mathbb{C}[V^*] serait non-dénombrable, es-tu d'accord avec la base que j'ai explicité plus haut ? Ex : loi...

Oui V^* est le dual de V . J'ai aussi beaucoup de mal à comprendre les données.. Je pense que : Si on suppose que V à une base \left\{ ei \right\}_{i \in I} , alors V^* a une base composée des \left\{ ei^* \right\}_{i \in I} . S(V) à pour base les \prod_{i \in I} e_i^{a_i} où les a_i sont pr...

Un polynôme n'est pas linéaire

Bonjour à tous, voici un exercice que je n'arrive pas à faire, je n'ai pas d'idée.. Soit V un ev Ici on note S(V) l'algèbre symétrique de V , et \Lambda(V) l'algèbre extérieure de V . on a une application: d_1 : S(V) \approx \mathbb{C}[V^*] \rightarrow S(V)^{\otimes 2...

Bonjour à tous,

est ce que quelqu'un pourrait m'expliquer pourquoi


Merci beaucoup et bonne journée

Bonjour à tous, je suis un peu perdu.. Supposons que l'on ait une algèbre de Lie réelle \mathfrak{h} ainsi qu'un espace vectoriel réel \mathfrak{m} . Posons \mathfrak{g} = \mathfrak{h}\oplus\mathfrak{m} Dans le document que j'étudie ils cherchent à construire un crochet [.,.] (pas de Lie, pour l'ins...

Je médite encore un peu sur les détails (genre d'où sortent les petit u et v) mais merci beaucoup, c'est super.

Ce sont des groupes !

Bonsoir à tous, je suis bloqué sur quelque chose..

J'aimerais montrer que dans le diagramme suivant, le produit fibré est bien G/UnV

Auriez-vous une idée ?



Merci beaucoup et bonne fin de soirée.

Et bien f est une fonction de R(G) c'est à dire que c'est une fonction de G dans .

Si G est cyclique les sont des racines de l'unité..

Bonjour à tous, je suis bloqué sur un exercice sur les transformations de Fourier et les reps de groupes.. Voici l'énoncé : Soit G un gp fini et \hat{G} l'ensemble des classes d'équivalences de ses représentations irréductibles complexes (de dim finie donc). Pour chaque i \in \hat{G} on choisit une ...

(Pourtant toutes les coniques non dégénérées sur un corps algébriquement clos sont équivalentes..) Ok merci de ta réponse, j'en ai encore une toute dernière concernant les courbes elliptiques.. En espérant que tu connaisses l'addition sur les cubiques projectives lisses ( http://www.math.jussieu.fr/...