661 résultats trouvés
Revenir à la recherche avancée
- 24 Nov 2007, 20:45
- Forum: ✯✎ Supérieur
- Sujet: égalité
- Réponses: 6
- Vues: 819
- 24 Nov 2007, 20:39
- Forum: ✯✎ Supérieur
- Sujet: égalité
- Réponses: 6
- Vues: 819
égalité
Bonsoir,
quelle démarche dois-je suivre pour montrer que :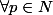 et
et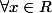
= (-1)^p\sum_{k=0}^{p}(-1)^k C_{2p+1}^k sin(2(p-k)+1)x)
merci
quelle démarche dois-je suivre pour montrer que :
merci
- 24 Nov 2007, 20:33
- Forum: ✯✎ Supérieur
- Sujet: égalité
- Réponses: 6
- Vues: 819
- 31 Mar 2007, 15:50
- Forum: ✯✎ Supérieur
- Sujet: s. Reiman
- Réponses: 3
- Vues: 457
s. Reiman
salut !
ça fait longtemps ! :lol4:
de retour avec une petite question :
en fait , je vois pas quelle fct prendre pour calculer la limite de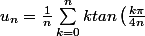) .
.
ben merci !
ça fait longtemps ! :lol4:
de retour avec une petite question :
en fait , je vois pas quelle fct prendre pour calculer la limite de
ben merci !
- 30 Mar 2007, 03:04
- Forum: ✯✎ Supérieur
- Sujet: s. Reiman
- Réponses: 3
- Vues: 457
Je dois trouver la dérivée de la fonction numérique suivante:
f(x)= (cos(x))²-cos(x)
euh encore et toujours la meme faute .. :soupir2:
- 12 Nov 2006, 16:23
- Forum: ✎✎ Lycée
- Sujet: Dérivée ...
- Réponses: 14
- Vues: 880
Le truc que je pige pas cest pourquoi cest \overline{({\vec{AC};\vec{AB}})} = Arg (\frac{b-a}{c-a}) + \frac{\pi}{2}[\pi] et non pas {({\vec{AC};\vec{AB}})} = Arg (\frac{b-a}{c-a}) + \frac{\pi}{2}[\pi] d'abord c'est \overline{(\vec{AC};\vec{AB})} \equiv \frac ...
- 12 Nov 2006, 12:54
- Forum: ✎✎ Lycée
- Sujet: Démontrer qu'un triangle est rectangle
- Réponses: 7
- Vues: 1262
Je comprends pas d'ou sort le "+ pi " cest pas plutot 'juste' modulo [2pi] ? on a Arg(-z) \equiv \pi + Arg(z) [2\pi] (c'est évident puisque M(z) et M(-z) sont symétrique par rapport O l'origine du repère ) donc ici Arg(- \frac{b-a}{c-a} ) \equiv \pi + Arg( \fra...
- 12 Nov 2006, 10:10
- Forum: ✎✎ Lycée
- Sujet: Démontrer qu'un triangle est rectangle
- Réponses: 7
- Vues: 1262
salut, 3$\frac{b-a}{c-a} = - \overline{\frac{b-a}{c-a}} donc 3$Arg\left(\frac{b-a}{c-a}\right) \equiv Arg \left(\overline{\frac{b-a}{c-a}}\right) + \pi [2\pi] i.e 3$Arg\left(\frac{b-a}{c-a}\right) \equiv - Arg \left({\frac{b-a}{c-a}}\right) + \pi [2\pi] ... je te lais...
- 11 Nov 2006, 14:01
- Forum: ✎✎ Lycée
- Sujet: Démontrer qu'un triangle est rectangle
- Réponses: 7
- Vues: 1262
- 04 Nov 2006, 20:52
- Forum: ✯✎ Supérieur
- Sujet: continuité
- Réponses: 8
- Vues: 806
- 04 Nov 2006, 20:41
- Forum: ✯✎ Supérieur
- Sujet: Fonction Arcsinus
- Réponses: 1
- Vues: 762
continuité
salut,
je bloque sur cet exo :
je dois étudier la continuité de la fonction f définie sur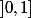 par :
par :
* = 0) si
si 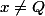
* = \frac{1}{p+q}) si
si 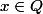
pourriez-vous m'aider ?
MERCI
je bloque sur cet exo :
je dois étudier la continuité de la fonction f définie sur
*
*
pourriez-vous m'aider ?
MERCI
- 30 Oct 2006, 23:08
- Forum: ✯✎ Supérieur
- Sujet: continuité
- Réponses: 8
- Vues: 806
bonjour, I(a,b) [FONT=Comic Sans MS] est centre de symétrie de [/FONT] C_f \Leftrightarrow \ \left\{ \begin{array}{ll} \forall x \in D_f \;\,\, 2a-x \in D_f \\ \forall x \in D_f \;\,\, f(2a-x) + f(x) = 2b\\ \end{array} \right. tu connais ça non ? il se voit que 8-x \in D_f do...
- 28 Oct 2006, 07:48
- Forum: ✎✎ Lycée
- Sujet: Exponentielle
- Réponses: 3
- Vues: 484
- 23 Oct 2006, 03:11
- Forum: ✯✎ Supérieur
- Sujet: une égalité
- Réponses: 8
- Vues: 674
- 23 Oct 2006, 02:57
- Forum: ✯✎ Supérieur
- Sujet: une égalité
- Réponses: 8
- Vues: 674
thx quand même Tize ! sinon j'ai une autre question j'espère qu'elle sera moins bête que la 1ère . je dois donner une forme simplifiée de S_n tel que : 3$ S_n = \sum_{k=1}^n Arctan\left(\frac{1}{k^2+k+1}\right) je sais pas par ou commencer :hein: PS : dsl je sais que c pas niveau sup .
- 22 Oct 2006, 23:37
- Forum: ✯✎ Supérieur
- Sujet: une égalité
- Réponses: 8
- Vues: 674
- 22 Oct 2006, 23:13
- Forum: ✯✎ Supérieur
- Sujet: une égalité
- Réponses: 8
- Vues: 674
- 22 Oct 2006, 22:57
- Forum: ✯✎ Supérieur
- Sujet: une égalité
- Réponses: 8
- Vues: 674
une égalité
salut, je veux démontrer : 3$\rm 2Arctan(\sqrt{1+x^2}-x) + Arctan x = \frac{\pi}{2} \forall x \in \mathbb{R} bon je suis arrivée jusqu'à : 3$2Arctan(\sqrt{1+x^2}-x) + Arctan x = Arctan(\sqrt{1+x^2}-x) + Arctan\left(\frac{1}{\sqrt{1+x^2} -x}\right) mais là je peux pas ...
- 22 Oct 2006, 22:53
- Forum: ✯✎ Supérieur
- Sujet: une égalité
- Réponses: 8
- Vues: 674
tize a écrit:???
Oui moi aussi j'ai beaucoup aimé le film...(le seul bon george lucas selon moi...) mais je ne vois pas le rapport...????
:ptdr:
thx=thanks , je suppose :lol2:
- 22 Oct 2006, 22:13
- Forum: ✯✎ Supérieur
- Sujet: Démontrer que x cos x < sin x
- Réponses: 13
- Vues: 1077
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
