Forum de Mathématiques: Maths-Forum

Oui ok, En fait si on restreint avec x>=0, alors le minimum est atteint en x=0,y=0.5 Mais en fait ce n'est qu'un exemple et ma question était plus générale que cela : est-il possible d'intégrer des contraintes de domaine pour des variables impliquées dans une recherche d'optimum par annulation des d...

Mais est-ce possible d'intégrer le fait que x et y >= 0 avec une méthode comme celle-ci?

ah zut oui, effectivement le minimum n'est pas (0,0.5)

Merci

Salut, Un problème de minimisation de fonction m'a amené à me poser des questions sur l'utilisation des dérivées. Plus particulièrement, je ne comprends pas la chose suivante : Soit la fonction f(x,y)=(x+y)^2-y qui accepte un minimum en (0,0.5). Je pensais retrouver ce résultat en ré...

Bonjour, Je me pose la question de savoir si une mesure d'angle entre des vecteurs (de dimension n) positifs non nuls (donc d'angle \leq \frac{\pi}{2} et \geq 0 ) peut être considérée comme une distance, en ce sens qu'elle respecte l'inégalité triangulaire : acos(\frac{\vec{u} . \vec{v}}{||\vec{...

Pour ta première question, comme les mesures des angles de vecteurs se calculent modulo 2pi, on a par exemple -pi/2=3pi/2 et cela fait que de parler d'inégalités entre des angles n'a en général pas beaucoup de sens... Pour ta deuxième question, la définition "carré carré" dit qu'un truc q...

Par contre, si l'on parle en terme d'angle, plutôt qu'en cosinus, les deux inégalités suivantes se vérifient elles d'après vous ? (\hat{\vec{u},\vec{v}}) \leq (\hat{\vec{u},\vec{w}}) + (\hat{\vec{v},\vec{w}}) (\hat{\vec{u},\vec{v}}) \geq | (\hat{\vec{u},\vec{w}}&...

Oui, c'est plutôt sin(\frac{\pi}{2}) qui est égal à 1, pas cos(\frac{\pi}{2}) qui lui est égal à 0... L'exemple donné par BEN314 contredit donc bien mon inégalité... tant pis pour moi :triste: Par contre, si l'on parle en terme d'angle, plutôt qu'en cosinus, les deux inégalités suiva...

Oups ! Au temps pour moi, en fait j'ai tout inversé... :hum: En fait, il faut raisonner en distances et non en proximité... Ce que je veux montrer c'est qu'il est toujours possible de former un triangle avec ces trois mesures de distances. Ces deux inégalités sont les deux conditions nécessaires pou...

Oui, en fait les vecteurs sont tous les trois de coordonnées positives ou nulles.

Le cosinus se formulant ainsi : , il est alors toujours ...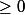

Une idée pour la démonstration de mes inégalités ?

Merci

Bonjour, J'ai besoin de montrer que, étant donnés trois vecteurs \vec{u},\vec{v},\vec{w} : cos(\vec{u},\vec{v}) \leq cos(\vec{u},\vec{w}) + cos(\vec{v},\vec{w}) cos(\vec{u},\vec{v}) \geq | cos(\vec{u},\vec{w}) - cos(\vec{v},\vec{w})| Quelqu'un aurait-i...

Oui, l'arbre total c'est ce que j'avais fait pour la première solution...et d'ailleurs je penchais plutôt pour cette solution mais cela me paraissait bizarre de tomber sur un résultat différent en énumérant toutes les possibilités... On a tout de même qu'un seul moyen d'avoir cette série et il y en ...

Salut, J'ai un problème pour calculer une proba, j'obtiens deux résultats différents selon la méthode de calcul que j'utilise, je ne sais pas peut être quelqu'un pourra m'éclairer... On dispose de deux urnes A et B. Dans A, il y a na boules blanches et dans B il y a nb boules noires. On tire success...

Personne n'a d'idée? Pensez vous que mon problème est insoluble (sans tester toutes les possibilités)?

Personne n'a d'idée? Pensez vous que mon problème est insoluble (sans tester toutes les possibilités)?

Personne n'a d'idée? Pensez vous que mon problème est insoluble (sans tester toutes les possibilités)?

Salut, Voici mon problème : On dispose de k urnes $u_1,u_2,...,u_k$ dont on tire des boules successivement et sans remise. Le nombre de boules contenues dans chaque urne $u_i$ avant de commencer les tirages est $n_i$ . A chaque tirage, le choix de l'urne est équiprobable mais lorsqu'une urne est vid...

Ok je reformule l'énoncé : n = nombre de boules total, $n_i$ = nombre de boules dans l'urne $u_i$ , k = nombre d'urnes, Trouver p(tirer la xième boule de u_i au tième tirage). Non Hydre, je ne pense pas que P(tirer la première boule dans A) = na/n, A chaque tirage, on a le choix entre les urnes qui ...

Merci pour cette analyse détaillée du problème,

mais ouais çà ne m'a pas l'air simple de trouver une formule générale...

Bonjour,

Je cherche à dénombrer le nombre de façons de disposer t boules dans k urnes, sachant que chaque urne u_i a une capacité c_i maximale (nombre de boules maximal que l'urne u_i peut contenir).

Quelqu'un a une idée?