Salut,
Voici mon problème :
On dispose de k urnes

dont on tire des boules successivement et sans remise. Le nombre de boules contenues dans chaque urne

avant de commencer les tirages est

. A chaque tirage, le choix de l'urne est équiprobable mais lorsqu'une urne est vide, elle est écartée (après que la première urne soit vide, on n'a plus le choix qu'entre k-1 urnes). Je cherche la probabilité de tirer la xième boule d'une urne donnée

au tième tirage.
Le problème est de savoir entre combien d'urnes on a à choisir à chaque tirage, tout dépend de ce qui a déjà été tiré...
Il y a bien moyen de trouver la réponse en essayant toutes les permutations mais il y en a beaucoup (

) et avec un grand nombre de boules et d'urnes, on risque de ne pas obtenir la réponse dans un temps raisonnable...
Je cherche donc une formule pour connaitre la probabilité de tirer la xième boule de
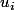
au tième tirage sans avoir à tester toutes les permutations... cela dépend, je pense, de la probabilité d'avoir tiré x-1 boules de
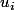
après t-1 tirages et de la probabilité de choisir l'urne

au tième tirage (qui dépend du nombre d'urnes non vides restantes...).
Quelqu'un a une idée?
