Vecteurs et cosinus

[tsinapah]

Bonjour,

J'ai besoin de montrer que, étant donnés trois vecteurs :

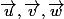
Quelqu'un aurait-il une idée ?

Merci d'avance

[gigamesh]

Bonjour,
un peu bizarre ta deuxième inégalité, car elle implique qu'un cosinus est toujours positif...
tu es sûr que tu ne nous as pas caché des informations sur les trois vecteurs ?

[tsinapah]

Oui, en fait les vecteurs sont tous les trois de coordonnées positives ou nulles.

Le cosinus se formulant ainsi : , il est alors toujours ...

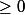
Une idée pour la démonstration de mes inégalités ?

Merci

[Ben314]

Salut,
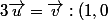Même en prenant les coordonnées positives, tes inégalités me parraissent douteuses : si dans le plan je prend et ta première inégalités dit que 1<=0+0....

[gigamesh]

En posant alpha=u,w beta=v,w on a u,v=alpha-beta (ce sont des angles tout ça)
Et d'après ce que tu disais sur les coordonnées, tout ce beau monde se balade entre 0 et pi/2 (ou plutôt -pi/2 et pi/2)

En tout cas on a que des cos et des sin positifs...
Du coup on a cos(alpha-beta)=cos(alpha)cos(beta)-sin(alpha)sin(beta) <= cos(alpha)cos(beta)

Bon évidemment on a le produit au lieu de la somme ; mais qd a,b sont dans [0;1] on a ab
Bon c'est un peu lourdaud comme méthode...

En tout cas la deuxième inégalité se prouve à partir de la première en utilisant la parité de cos, je pense (donc en échangeant u et v)

[tsinapah]

Oups !
Au temps pour moi, en fait j'ai tout inversé... :hum:
En fait, il faut raisonner en distances et non en proximité... Ce que je veux montrer c'est qu'il est toujours possible de former un triangle avec ces trois mesures de distances. Ces deux inégalités sont les deux conditions nécessaires pour construire un triangle de trois points séparés par ces trois distances...

Bon, je la refais :

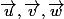
J'ai besoin de montrer que, étant donnés trois vecteurs positifs non nuls (de norme > 0) :

Désolé...

[Ben314]

Ben...
En prenant u:(1,0) ; v:(0,1) et w:(1,1), ton inégalité 1) donne c'est à dire ...

[gigamesh]

En posant a=cos alpha = cos u,w et b= cos beta = cos v,w
il vient cos(u,v)=cos(alpha-beta)=cos(alpha)cos(beta)+sin(alpha)sin(beta)
cos(u,v)=ab+rac(1-a²)rac(1-b²).

Ton inégalité équivaut donc à a+b-ab-rac(...)rac(...) <=1
soit a+b-ab-1 <= rac(...)rac(...),
inégalité qui est triviale à démontrer une fois qu'on a remarqué
que a+b-ab-1=-(1-a)(1-b) ...

[gigamesh]

Ben...
En prenant u:(1,0) ; v:(0,1) et w:(1,1), ton inégalité 1) donne c'est à dire ...

ici (u,v)=pi/2 et cos pi/2 = 1 donc le membre gauche est 1-1, non ?

[Ben314]

C'est pas faux...
Mais de ton coté, tu pioche où que les sinus sont positifs (i.e. égaux à racine(1-cos²)) et qu'ils ne sont pas négatifs ?

Edit : J'avais commencé à écrire ça :

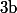
Si on note et des mesures des angles (orientés) et , ton inégalité 1) s'écrit :



si on suppose

Sauf que je ne vois pas de raison que cette dernière inégalité soit vérifiée.

REEDIT : Tu est vraiment sûr que cos(pi/2)=1 ?????

[tsinapah]

Oui, c'est plutôt qui est égal à 1, pas qui lui est égal à 0...

L'exemple donné par BEN314 contredit donc bien mon inégalité... tant pis pour moi :triste:



Par contre, si l'on parle en terme d'angle, plutôt qu'en cosinus, les deux inégalités suivantes se vérifient elles d'après vous ?

Là, çà marche non ?

En tout cas, merci beaucoup à tous les deux de vous intéresser à mon problème... :happy2:

Edit : Y a t'il un terme pour qualifier une mesure de distance qui ne vérifie pas ce genre d'inégalités , c'est à dire que les distances calculées entre trois points ne permettent pas de dessiner un triangle ? inégalité triangulaire ?

[gigamesh]

Oh la la je suis nul !
Bon ouais évidemment cos(pi/2)=0 !!!! (je n'ai pas dit 0 factorielle factorielle factorielle factorielle, qui vaut 1, ce sont juste des points d'exclamation).

Bon les sin sont positifs car les angles sont dans [0;pi/2].
Je ne vois pas où est mon erreur.

Bon, la nuit porte conseil.

[tsinapah]

Par contre, si l'on parle en terme d'angle, plutôt qu'en cosinus, les deux inégalités suivantes se vérifient elles d'après vous ?

Oui, bon la seconde inégalité découle de la première. Si on a :





et



On a :



et



Et donc on a :



La première inégalité correspond à une inégalité triangulaire sur les distances :



La question revient donc à se demander si une mesure d'angle entre des vecteurs vérifie bien l'inégalité triangulaire... Est-ce bien le cas d'après vous ? Y a t'il des conditions à respecter sur les vecteurs ?

[Ben314]

Pour ta première question, comme les mesures des angles de vecteurs se calculent modulo 2pi, on a par exemple -pi/2=3pi/2 et cela fait que de parler d'inégalités entre des angles n'a en général pas beaucoup de sens...

Pour ta deuxième question, la définition "carré carré" dit qu'un truc qui ne vérifie pas l'inégalité triangulaire, ben normalement, on n'as pas le droit de l'appeller "distance" (Définition : une distance est une application de ExE dans R+ telle que ...)

[Ben314]

En posant a=cos alpha = cos u,w et b= cos beta = cos v,w...

Les vecteurs u,v,w étant dans le même quart de plan, tout ce que tu peut dire de tes angles alpha et beta, c'est qu'ils sont entre -pi/2 et pi/2 ce qui n'implique nullement que leurs sinus sont positifs...

[tsinapah]

Pour ta première question, comme les mesures des angles de vecteurs se calculent modulo 2pi, on a par exemple -pi/2=3pi/2 et cela fait que de parler d'inégalités entre des angles n'a en général pas beaucoup de sens...

Pour ta deuxième question, la définition "carré carré" dit qu'un truc qui ne vérifie pas l'inégalité triangulaire, ben normalement, on n'as pas le droit de l'appeller "distance" (Définition : une distance est une application de ExE dans R+ telle que ...)

Ok mais ici je ne parle pas d'angles orientés... et sur des vecteurs positifs (donc avec un angle maximal de ). Autrement dit . Sous ces contraintes, la mesure d'angle vérifie-t-elle l'inégalité triangulaire ?

Je peux peut-être définir l'application suivante pour clarifier : est une application de dans , telle que

Je me pose alors la question de savoir si peut être considérée comme une distance, c'est à dire qu'elle vérifie l'inégalité triangulaire qui m'intéresse (les propriétés de symétrie et de séparation étant vérifiées de manière triviale...)

Merci