8 résultats trouvés
Revenir à la recherche avancée
Merci tournesol pour les encouragements

catamat Oui en effet j'ai recopié de ma feuille et j'ai oublié de remettre le
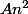
bien vu

Je viens de recoriger au cas ou un autre étudiant voudrais refaire l'exo pour comparer
- par alexisdgv
- 30 Oct 2021, 15:14
-
- Forum: ✯✎ Supérieur
- Sujet: Démonstration par recurrence non homogène
- Réponses: 7
- Vues: 438
Merci tournesol, en effet j'ai oublié de multiplié par n dans la résolution de la partie homogène Après correction: Partie homogène: x^2 - 2x + 1 = 0 \delta : b^2 - 4ac = 4 - 4 * 1 *1 = 0 -b/2a = 2/2 = 1 (x-1)^2 U_h : \alpha(1)^n + \beta * n* (1)^n Partie non homogène: Forme ...
- par alexisdgv
- 29 Oct 2021, 20:49
-
- Forum: ✯✎ Supérieur
- Sujet: Démonstration par recurrence non homogène
- Réponses: 7
- Vues: 438
Merci oui j'ai bien A= 1/2 mais apres j'ai des problèmes pour avoir la solution complète quand j'essaie avec les valeurs de départ. Je vais peut-être remettre les détails de mes calculs: Partie homogène: x^2 - 2x + 1 = 0 \delta : b^2 - 4ac = 4 - 4 * 1 *1 = 0 -b/2a = 2/2 = 1 (x-1)^2 U_h : \al...
- par alexisdgv
- 29 Oct 2021, 18:44
-
- Forum: ✯✎ Supérieur
- Sujet: Démonstration par recurrence non homogène
- Réponses: 7
- Vues: 438
Bonjour, je dois résoudre le système d'équation de récurrence non homogène définis pour : n \in \N : u_{n+2} +u_n - 2u_{n+1} =1 u_0=1/2 u_1=0 Pour la partie homogène j'ai ceci: x^2-2x+1 =0 je calcule Delta: (-2)^2 =4 - 4ac = 4 - 4 .1 =0 donc une seule racine ici -b/2a c'est a dire 2 /2 =1 (x-1)^2 do...
- par alexisdgv
- 29 Oct 2021, 13:30
-
- Forum: ✯✎ Supérieur
- Sujet: Démonstration par recurrence non homogène
- Réponses: 7
- Vues: 438
Merci en fait c'est bien une suite qu'il faut faire c'était marqué qu'il faut considérer l’indice j de 1 à 2(n + 1) − 1 est identique de considérer l’indice j de 1 à 2n − 1 puis l’indice j = 2n et ensuite j = 2n + 1.
- par alexisdgv
- 18 Oct 2021, 19:46
-
- Forum: ✯✎ Supérieur
- Sujet: Démonstration par récurrence
- Réponses: 2
- Vues: 242
Bonjour, Pour la démonstration par récurrence de ceci: \forall n \in \N_0: \sum_{j=1}^{2n-1}{(-1)^{j-1} j^2 } = n(2n -1) Dans l'hérédité on veut démontrer au rang suivant, pourquoi on prend le rang actuel + le suivant + encore le suivant? Est-ce a cause du 2n-1 ? Pour avoir le terme ...
- par alexisdgv
- 18 Oct 2021, 08:20
-
- Forum: ✯✎ Supérieur
- Sujet: Démonstration par récurrence
- Réponses: 2
- Vues: 242
Bonjour, j'ai la proposition suivante qu'on doit démontrer sans table de vérité qu'il s'agit bien d'une tautologie: {(p=>q V (r ⊕ p)) => ( ¬q ∧ r)} <=> ( ¬q ∧ r) En isolant la partie de gauche de l'équivalence, Je comprends pour arriver à cela {(p ∧ non(q V (r ⊕ p)) ∨ ( ¬q ∧ r)} je comprends pas com...
- par alexisdgv
- 18 Oct 2021, 08:05
-
- Forum: ✯✎ Supérieur
- Sujet: Exercice technique de démonstration
- Réponses: 3
- Vues: 315