Forum de Mathématiques: Maths-Forum

supposer qu'il y'en a deux et arriver à une contradiction par rapport à la minoration de f '

je ne suis pas très sûr du sens de 'lipschitzienne' mais l'unicité du point fixe peut être montrée grâce à l'inégalité des accroissements finis il me semble

nanan, je suis tout à fait convaincu de la véracité de cette propriété (d'où la question 'bête'), seulement un schéma n'aura jamais toute la puissance d'une démonstration toute brutale, et c'est ca qui me manque...

comment je peux démontrer que, si f est continue sur ]a,b[, quelque soit la valeur attribuée à f(a) et à f(b), l'intégrale de f entre a et b aura toujours la même valeur ?
merci

ton problème est régle. Si je reprends tes notations et que je pose n=deg(P) on a : P(A)=somme de k=0 à n de alpha(k)A^k =somme de k=0 à n de alpha(k)(T^-1)(Q^k)T =(T^-1)(somme de k=0 à n de alpha(k)(Q^k))T Or les alpha(k)Q^k sont toutes diagonales, leur somme est donc diagonale. Donc P(A)=(T^-1)DT ...

Ben tu as une loi normale dont les paramètres sont donnés, et tu veux a tel que P([X>a])=0,1 Tu ramènes X à une loi normale centrée réduite X'=(X-32,3)/8,5, tu fouilles ton tableau de valeurs pour la loi normale centrée réduite et tu sors la solution de l'équation P([X'>a'])=0,1 (cela dit mon progra...

oui, oui, je connais le raisonnement par analyse-synthèse, seulement l'énoncé présente explicitement la question comme si il fallait d'abord prouver l'existence de alpha(r) puis l'exprimer en fonction de r et U(r)... En tout cas merci pour votre aide rapide et efficace :) (et fatal_error, tu devrais...

mais attend, il me semble que, si je lis bien, la question consiste à démontrer que l'égalité : U(n)=n^alpha(r) est vraie (qu'il existe effectivement un tel alpha(r)) or tu pars du principe que c'est déjà effectivement vérifié... est-ce moi qui lit mal l'énoncé ? edit : pour être honnête il me sembl...

de la relation précédente je déduis donc :
U(n)=U(r^k)=(U(r))^k
mais je vois toujours pas comment le n (i.e. le r^k) va apparaître autrement qu'en tant qu'indice ? quels sont les deux membres élevés à la puissance k dont tu parles ? je crois que j'ai pas bien tout saisi...

Je rencontre un petit problème dans la résolution de cette annale de concours : http://www.bankexam.fr/annales/1626_HEC_2004_concours.pdf Partie I question 3, Soit r élément de N*, r > 2. Montrer qu’il existe un réel alpha(r) tel que, pour tout entier n de la forme n = r^k où k est un entier positif...

comme ca j'ai une solution algébrique et une solution analytique ^^ merci les gars (je suppose) c'était super

brillant, merci...

euh, j'ai fait le calcul, et je mentionnais justement poliment que ta marche à suivre ne pouvait en aucun cas être la bonne...
(et j'espère sincèrement ne pas t'avoir froissé, j'apprécie énormément ton aide)

Ca m'embêterait, ca voudrait dire qu'on trouve 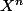alors qu'on veut prouver que ca vaut
Bref l'idée est brillante mais le calcul me semble faux puisqu'il reste un (factoriel i) qui traine et empêche une simplification du binôme...

dimension infinie donc pas de représentation matricielle possible, non ?

J'ai une peine incroyable à démontrer ce résultat : On sait que pour tout n entier naturel : L_n = \sum_{k=0}^n (^{n}_{k}) (-1)^k \frac{X^k}{k!} et que L_n(0) = 1 (il s'agit du n_ème polynôme de Laguerre...) Montrer que pour tout n entier naturel, \frac{X^n}{n!} = \sum_{k=0}^...

Bon, certes cela date un peu, mais j'ai dû résoudre cet exercice aujourd'hui alors je mets la réponse, ca peut servir à d'autres : En effet, Xo est pseudo solution si et ssi AXo est le projeté orthogonal de B sur Im(A) (immédiat grâce au théorème de meilleure approximation) Partant, la caractérisati...