Question bête sur les intégrales
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
JCardan
- Membre Naturel
- Messages: 17
- Enregistré le: 02 Jan 2008, 19:24
-
 par JCardan » 27 Avr 2008, 18:42
par JCardan » 27 Avr 2008, 18:42
comment je peux démontrer que, si f est continue sur ]a,b[, quelque soit la valeur attribuée à f(a) et à f(b), l'intégrale de f entre a et b aura toujours la même valeur ?
merci
-
rafbh
- Membre Relatif
- Messages: 250
- Enregistré le: 19 Nov 2006, 17:07
-
 par rafbh » 27 Avr 2008, 19:00
par rafbh » 27 Avr 2008, 19:00
L'intégrale est la somme entre la courbe et l'axe!Donc la disconuité en un nombre fini de points n'affecte pas cette somme!
oki?
fais un schéma
-
JCardan
- Membre Naturel
- Messages: 17
- Enregistré le: 02 Jan 2008, 19:24
-
 par JCardan » 27 Avr 2008, 19:01
par JCardan » 27 Avr 2008, 19:01
nanan, je suis tout à fait convaincu de la véracité de cette propriété (d'où la question 'bête'), seulement un schéma n'aura jamais toute la puissance d'une démonstration toute brutale, et c'est ca qui me manque...
-
rafbh
- Membre Relatif
- Messages: 250
- Enregistré le: 19 Nov 2006, 17:07
-
 par rafbh » 27 Avr 2008, 19:04
par rafbh » 27 Avr 2008, 19:04
Pour la démo fais un tour chez wiki.
l'dée c'est de discuter selon les valeurs de f(a)et de f(b) et d'ajouter des points dans la subdivision!
 par busard_des_roseaux » 27 Avr 2008, 21:13
par busard_des_roseaux » 27 Avr 2008, 21:13
bjr,
avec l'intégrale de riemmann (généralisée),
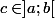
 dt = \lim_{x \rightarrow b^{ -}} \int_{c}^{x} f(t)dt)
la définition ne dépend pas de f(b).
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 27 Avr 2008, 22:04
par ffpower » 27 Avr 2008, 22:04
Pour la preuve,tout dépend de ta definition de l integrale en fait
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
