Egalité à prouver (Polynômes de Laguerre)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
JCardan
- Membre Naturel
- Messages: 17
- Enregistré le: 02 Jan 2008, 19:24
-
 par JCardan » 04 Jan 2008, 12:37
par JCardan » 04 Jan 2008, 12:37
J'ai une peine incroyable à démontrer ce résultat :
On sait que pour tout n entier naturel :
 (-1)^k \frac{X^k}{k!})
et que
 = 1)
(il s'agit du n_ème polynôme de Laguerre...)
Montrer que pour tout n entier naturel,
 (-1)^k L_k)
j'ai du louper le truc évident, bref j'ai le sentiment de tourner en rond, impossible de boucler une quelconque récurrence ou quoique ce soit, c'est à se frapper la tête contre les murs... tout indice est le bienvenu ! Merci d'avance
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
 par fenecman » 04 Jan 2008, 14:24
par fenecman » 04 Jan 2008, 14:24
ça me rappelle quelque chose mais je suis pas sur.
Tu connais la decomposition des Ln dans la base X^k/k!
Si t'écrit la matrice correspondante et que tu l'inverse t'aura les X^k/k! en fonction des Lk .
Enfin c'est une idée , faut voire la matrice!!
-
JCardan
- Membre Naturel
- Messages: 17
- Enregistré le: 02 Jan 2008, 19:24
-
 par JCardan » 04 Jan 2008, 14:36
par JCardan » 04 Jan 2008, 14:36
dimension infinie donc pas de représentation matricielle possible, non ?
 par busard_des_roseaux » 04 Jan 2008, 16:46
par busard_des_roseaux » 04 Jan 2008, 16:46
JCardan a écrit:Montrer que pour tout n entier naturel,
 (-1)^k L_k)
bjr,
on part de cette somme. On remplace L_k par sa formule avec

(écrire unsecond indice i).
Les deux coefficients du binome se simplifient un peu.
On trouve finalement en arrangeant:
 {(-1)}^k {(1-x)}^k = {\left( 1-(1-x) \right)}^n)
-
JCardan
- Membre Naturel
- Messages: 17
- Enregistré le: 02 Jan 2008, 19:24
-
 par JCardan » 04 Jan 2008, 16:55
par JCardan » 04 Jan 2008, 16:55
Ca m'embêterait, ca voudrait dire qu'on trouve
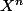
alors qu'on veut prouver que ca vaut

Bref l'idée est brillante mais le calcul me semble faux puisqu'il reste un (factoriel i) qui traine et empêche une simplification du binôme...
 par busard_des_roseaux » 04 Jan 2008, 16:57
par busard_des_roseaux » 04 Jan 2008, 16:57
JCardan a écrit:Ca m'embêterait, ca voudrait dire qu'on trouve
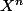
alors qu'on veut prouver que ca vaut

Bref l'idée est brillante mais le calcul me semble faux puisqu'il reste un (factoriel i) qui traine et empêche une simplification du binôme...
exact, autant pour moi, c'est faux. :hum:
-
JCardan
- Membre Naturel
- Messages: 17
- Enregistré le: 02 Jan 2008, 19:24
-
 par JCardan » 04 Jan 2008, 16:59
par JCardan » 04 Jan 2008, 16:59
euh, j'ai fait le calcul, et je mentionnais justement poliment que ta marche à suivre ne pouvait en aucun cas être la bonne...
(et j'espère sincèrement ne pas t'avoir froissé, j'apprécie énormément ton aide)
 par busard_des_roseaux » 04 Jan 2008, 17:56
par busard_des_roseaux » 04 Jan 2008, 17:56
JCardan a écrit:Montrer que pour tout n entier naturel,
 (-1)^k L_k)
ça y est, cette fois, c'est ok. On pose:

 (-1)^k L_k)
Pour montrer l'égalité entre ces deux polynomes de degré n, il suffit, en pensant à laformule de Taylor, exacte au rang n, pour les polynomes de degré n, il suffit donc de montrer que leur nombres dérivés à l'ordre p
sont égaux en x=0 , pour
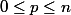
, c'est à dire:
}(0)=B_{n}^{(p)}(0))
Côté gauche, le polynôme
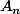
admet en x=0 un zéro d'ordre n.
Pour ce qui concerne le côté droit,
on calcule d'abord les nombres dérivés:
} = 0)
si p > n cad si n < p.
}(0) = {(-1)}^p (_{p}^n))
si
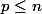
cad si
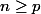
.
 par busard_des_roseaux » 04 Jan 2008, 18:06
par busard_des_roseaux » 04 Jan 2008, 18:06
Il ne reste plus quà montrer que
a)
}(0)=0 pour 0 \leq p < n)
b)
}(0)=1)
Pour (b):
}(0)=(-1)^n \times (-1)^n=1)
pour (a):
pour

}(0)=\sum_{k=0}^{n} \, (_{k}^{n}) {(-1)}^k L_{k}^{(p)}(0)=\sum_{k=p}^{n} \, (_{k}^{n}) {(-1)}^k {(-1)}^{p} (_{p}^{k}) =\frac{n!}{p!} \sum_{u=0}^{n-p} \, {(-1)}^u \frac{1}{u! (n-p-u)!}=0)
Les deux polynômes sont égaux car leurs nombres dérivés jusqu'à l'ordre
n, calculés en x=0, sont égaux.
CQFD. :zen:
-
JCardan
- Membre Naturel
- Messages: 17
- Enregistré le: 02 Jan 2008, 19:24
-
 par JCardan » 04 Jan 2008, 18:18
par JCardan » 04 Jan 2008, 18:18
brillant, merci...
-
fenecman
- Membre Relatif
- Messages: 139
- Enregistré le: 11 Nov 2006, 15:50
-
 par fenecman » 04 Jan 2008, 19:13
par fenecman » 04 Jan 2008, 19:13
Je pense qu'avec la matrice il y avait moyen aussi, je m'explique:
On écrit les (L0,.....,Ln) dans la base des (1,X,....,X^n/n!)
Mais cette matrice est aussi la matrice de l'endomorphisme f de Rn[X] dans la base canonique de Rn[X] tel que (f(P))(X) = P (1-X)
Mais f(f(P))(X)=P(1-(1-X))=P(X)
donc l'inverse de cette matrice est elle-meme donc en lisant la derniere colonne de la matrice inverse on a X^n/n! = la bonne chose.
-
JCardan
- Membre Naturel
- Messages: 17
- Enregistré le: 02 Jan 2008, 19:24
-
 par JCardan » 05 Jan 2008, 00:47
par JCardan » 05 Jan 2008, 00:47
comme ca j'ai une solution algébrique et une solution analytique ^^ merci les gars (je suppose) c'était super
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
