11 résultats trouvés
Revenir à la recherche avancée
Re: Intégrale divergente coordonnées polaires
Voyons, penses-tu que \displaystyle\int_0^1\dfrac{dx}{\sqrt x} diverge ? Non bien évidemment cette intégrale converge, intégrale de Riemann avec 1/2 < 1 Une intégrale, dans cette configuration, c'est un peu comme un volume. Tu imagines un volume en forme de vase, limité par un rayon de 1 par exempl...
- 20 Mai 2022, 23:34
- Forum: ✯✎ Supérieur
- Sujet: Intégrale divergente coordonnées polaires
- Réponses: 7
- Vues: 411
Re: Intégrale divergente coordonnées polaires
Je pensais que comme on ne pouvait pas la définir en (0,0) et qu'elle présentait une asymptote verticale alors elle était divergente, mais au final ce n'est pas le cas je pense.
Merci !
Merci !
- 20 Mai 2022, 20:38
- Forum: ✯✎ Supérieur
- Sujet: Intégrale divergente coordonnées polaires
- Réponses: 7
- Vues: 411
Re: Intégrale divergente coordonnées polaires
Il n y a pas d'énoncé justement, c'est juste une fonction que j'étudie. C'est pour ça que je suis perturbé parce qu'en l'infini il y a une décroissance lente donc divergence mais en 0 il y a également une asymptote verticale donc pas de convergence... elle est localement intégrable en revanche. Mon ...
- 20 Mai 2022, 14:57
- Forum: ✯✎ Supérieur
- Sujet: Intégrale divergente coordonnées polaires
- Réponses: 7
- Vues: 411
Intégrale divergente coordonnées polaires
Bonjour, Je ne trouve pas comment montrer que l'intégrale suivante diverge en (0,0). \int_{\mathbb{R}^2} \frac{1}{\sqrt{x^2+y^2}}dxdy Je passe en coordonnées polaires et j'obtiens : \int_0^{2 \pi} \int_{[rayon]} \frac{1}{\sqrt{r^2}}rdrd\theta = 2 \pi \int_{[rayon]} 1 dr et cette intégrale est bien d...
- 20 Mai 2022, 12:34
- Forum: ✯✎ Supérieur
- Sujet: Intégrale divergente coordonnées polaires
- Réponses: 7
- Vues: 411
Re: Projection orthogonale
Ah oui... en effet, merci j'avais très mal écrit ma solution
- 28 Jan 2022, 00:30
- Forum: ✯✎ Supérieur
- Sujet: Projection orthogonale
- Réponses: 4
- Vues: 318
Re: Projection orthogonale
Merci pour ta réponse.
Je prends comme norme |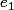 | = 1 /
| = 1 /  et donc (1 /
et donc (1 /  , 1 /
, 1 /  ) comme
) comme 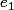 . Mais au final cela ne me débloque pas et je n'obtiens pas (5/2, 5/2).
. Mais au final cela ne me débloque pas et je n'obtiens pas (5/2, 5/2).
Je prends comme norme |
- 27 Jan 2022, 22:21
- Forum: ✯✎ Supérieur
- Sujet: Projection orthogonale
- Réponses: 4
- Vues: 318
Projection orthogonale
Bonjour, J'écris ce message car je ne comprends très bien le théorème de projection orthogonale. En effet imaginons qu'on ait un sous-espace vectoriel de R tel que E = {(x, y) dans R² | x = y}. Si on voulait calculer projeté orthogonal de (3, 2) on devrait obtenir (2.5, 2.5) car il minimise ||(3, 2)...
- 27 Jan 2022, 20:17
- Forum: ✯✎ Supérieur
- Sujet: Projection orthogonale
- Réponses: 4
- Vues: 318
Re: Fonction de plusieurs variables polaires
Oh d'accord merci!
- 16 Juin 2021, 00:40
- Forum: ✯✎ Supérieur
- Sujet: Fonction de plusieurs variables polaires
- Réponses: 7
- Vues: 362
Fonction de plusieurs variables polaires
Bonjour, Je vous envoie ce message car je n'arrive pas à montrer la continuité d'une fonction de plusieurs variables en polaire. Il nous est demandé de prouver la continuité en 0 de la fonction https://i.ibb.co/sjBMVfF/image.png Je passe donc au polaire https://i.ibb.co/7ybVnqh/image.png J'obtiens d...
- 15 Juin 2021, 19:28
- Forum: ✯✎ Supérieur
- Sujet: Fonction de plusieurs variables polaires
- Réponses: 7
- Vues: 362
Re: Questions de probabilités
92 : supposons qu'on tire une boule blanche dans la première on a donc la probabilité d'avoir une boule blanche dans U1 qui est (3n - 1) / (4n - 1) et dans la deuxième urne (3n + 1) / (4n + 1) Supposons à l'inverse qu'on tire une noire dans la première on a donc la probabilité d'avoir une boule blan...
- 12 Avr 2021, 22:31
- Forum: ✯✎ Supérieur
- Sujet: Questions de probabilités
- Réponses: 3
- Vues: 234
Questions de probabilités
Bonjour à tous, Je me permets d'envoyer ce message car j'aurais deux questions à résoudre en probas/stats... j'ai un peu de difficulté à y répondre donc je vous joins une photo de l'énoncé. Il peut y avoir plusieurs réponses possibles. https://i.ibb.co/k9vMjD8/Capture.png Merci d'avance !
- 12 Avr 2021, 19:56
- Forum: ✯✎ Supérieur
- Sujet: Questions de probabilités
- Réponses: 3
- Vues: 234
- 11 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
