10 résultats trouvés
Revenir à la recherche avancée
Densité de l'ensemble des nombres de Liouville
Bonjour, je souhaiterais montrer que l'ensemble \mathcal{L} des nombres de Liouville est dense dans \mathbb{R} . En effet je sais que \mathcal{L}=\bigcap_{n\in\mathbb{N}}\mathcal{O}_n , où \mathcal{O}_n=\bigcup_{\underset{b\ge2}{(a,b)\in\mathbb{Z}^2}}]\frac{a}{b}-\frac{1}{b^n},\frac{a}{b}+\f...
- 06 Juin 2019, 14:46
- Forum: ✯✎ Supérieur
- Sujet: Densité de l'ensemble des nombres de Liouville
- Réponses: 1
- Vues: 317
Re: Probas discrètes, dénombrement
Oui, j'ai un peu trop arrondi, mais merci beaucoup ça me rassure quant à mon raisonnement
- 08 Mar 2019, 16:57
- Forum: ✯✎ Supérieur
- Sujet: Probas discrètes, dénombrement
- Réponses: 4
- Vues: 311
Probas discrètes, dénombrement
Bonjour, J’aimerais avoir votre avis sur un petit exercice de dénombrement, j’ai un doute quant au résultat que j’ai obtenu On considère un paquet de 32 cartes (le fameux) et on effectue un tirage de 4 cartes réparties de manière équiprobable. On demande, parmi les questions, la probabilité que l’on...
- 08 Mar 2019, 16:21
- Forum: ✯✎ Supérieur
- Sujet: Probas discrètes, dénombrement
- Réponses: 4
- Vues: 311
Re: Cardinal d'une classe d'équivalence
Voilà, je me disais bien que je manquais quelque chose, merci infiniment
Evidemment les éléments de la classe de a qui vérifient l'équation existent si et seulement si l'équation de degré 2 existe
Ça nous fait donc deux représentants par classe pour tout élément non nul différent de -2 et -1
Evidemment les éléments de la classe de a qui vérifient l'équation existent si et seulement si l'équation de degré 2 existe
Ça nous fait donc deux représentants par classe pour tout élément non nul différent de -2 et -1
- 16 Jan 2019, 14:10
- Forum: ✯✎ Supérieur
- Sujet: Cardinal d'une classe d'équivalence
- Réponses: 7
- Vues: 1691
Re: Cardinal d'une classe d'équivalence
Effectivement, 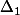 ne s'annule qu'en
ne s'annule qu'en 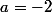 , ce qui m'intrigue c'est que pourtant
, ce qui m'intrigue c'est que pourtant  n'est pas racine de
n'est pas racine de 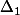 mais ne compte qu'un seul représentant dans sa classe d'équivalence, à savoir lui même
mais ne compte qu'un seul représentant dans sa classe d'équivalence, à savoir lui même
- 16 Jan 2019, 14:01
- Forum: ✯✎ Supérieur
- Sujet: Cardinal d'une classe d'équivalence
- Réponses: 7
- Vues: 1691
Re: Cardinal d'une classe d'équivalence
Et je ne vois évidemment pas où est-ce que j’ai fait une erreur
- 16 Jan 2019, 13:36
- Forum: ✯✎ Supérieur
- Sujet: Cardinal d'une classe d'équivalence
- Réponses: 7
- Vues: 1691
Re: Cardinal d'une classe d'équivalence
Justement, c’est là où ça me pose un problème c’est que ça n’est pas cohérent avec ce que j’ai fait
- 16 Jan 2019, 13:32
- Forum: ✯✎ Supérieur
- Sujet: Cardinal d'une classe d'équivalence
- Réponses: 7
- Vues: 1691
Cardinal d'une classe d'équivalence
Bonjour, j'ai un doute sur une question sur les classes d'équivalence et je souhaiterais savoir si mon raisonnement est juste Soit \mathcal{R} une relation d'équivalence sur \mathbb{R}^* définie par x\mathcal{R}y\iff\frac{x+1}{x^2}=\frac{y+1}{y^2} On voit donc que [-1]_{\mathcal{R}}={-1\} Maintenant...
- 16 Jan 2019, 13:13
- Forum: ✯✎ Supérieur
- Sujet: Cardinal d'une classe d'équivalence
- Réponses: 7
- Vues: 1691
Cardinal d'une classe d'équivalence
Bonjour, j'ai un doute sur une question sur les classes d'équivalence et je souhaiterais savoir si mon raisonnement est juste
Soit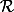 une relation d'équivalence sur
une relation d'équivalence sur 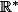 définie par
définie par 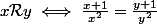
On voit donc que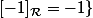
Soit
On voit donc que
- 16 Jan 2019, 13:06
- Forum: ✯✎ Supérieur
- Sujet: Cardinal d'une classe d'équivalence
- Réponses: 1
- Vues: 505
Lois de Morgan, complémentaires
Bonjour, je souhaitais savoir si l'on pouvait montrer des égalités avec les complémentaires sans passer par la double inclusion mais uniquement par équivalence logique, comme ceci: x\in \complement_E(A\cap B)\iff x\notin A\cap B\iff (x\notin A) \vee (x\notin B)\\ \iff (x\...
- 17 Oct 2018, 13:38
- Forum: ✯✎ Supérieur
- Sujet: Lois de Morgan, complémentaires
- Réponses: 2
- Vues: 545
- 10 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
