Densité de l'ensemble des nombres de Liouville

[Jeejsaas]

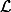
Bonjour, je souhaiterais montrer que l'ensemble des nombres de Liouville est dense dans .
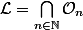
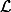
En effet je sais que , où . Le fait que soit dense ne pose pas de problème, donc je peux utiliser le théorème de Baire pour conclure que est dense dans .

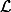
Cependant je ne vois pas comment montrer que admet cette décomposition comme intersection d'ouverts ; je sais uniquement que en considérant une reformulation du théorème de Liouville, cela me permet de montrer que si est de Liouville, alors il existe une suite de rationnels à support infini telle que , ce qui est équivalent à ce que .

Quelqu'un pourrait-il éclairer ma lanterne? Je vous remercie d'avance

[GaBuZoMeu]

En fait, est de Liouville si et seulement s'il existe une suite de rationnels telle que .