10 résultats trouvés
Revenir à la recherche avancée
Re: Intégrale
Salut On a f:I\to \R , une application continue et \phi une application \mathcal{C}^1 telle que \phi([a,b])\subset I , alors : \int_a^bf\big(\phi(t)\big).\phi'(t)\cdot dt=\int_{\phi(a)}^{\phi(b)} f(s)\cdot ds On identifie ta fonction : f: y...
- 09 Aoû 2019, 21:02
- Forum: ✯✎ Supérieur
- Sujet: Intégrale
- Réponses: 11
- Vues: 432
Re: Demonstration nombres complexes
Bonjour

et
et
- 26 Juil 2019, 11:04
- Forum: ✯✎ Supérieur
- Sujet: Demonstration nombres complexes
- Réponses: 5
- Vues: 462
Re: image d'un réel
Je ne pense pas que tu trouveras une définition de +\infty comme tu le souhaites... Par contre tu trouveras des définitions du genre : \lim_{x\to +\infty}f(x)=+\infty\iff \forall A>0, \exists x_0\in \mathcal{D}_f, \forall x \in \mathcal{D}_f,\quad x>x_0\implies f(x)>A Tu remarqueras ...
- 08 Juil 2019, 00:02
- Forum: ✯✎ Supérieur
- Sujet: image d'un réel
- Réponses: 21
- Vues: 1159
Re: image d'un réel
si  est défnie en
est défnie en  , il existe un unique réel
, il existe un unique réel  tel que
tel que =y)
- 07 Juil 2019, 08:52
- Forum: ✯✎ Supérieur
- Sujet: image d'un réel
- Réponses: 21
- Vues: 1159
Re: image d'un réel
La définition d'une application. f:E\to F \forall x \in E, \exists ! y\in F, \; f(x)=y La fonction x\mapsto \frac{1}{x} n'est pas défnie en 0. La recherche de l'ensemble de définition permet de définir une application à partir de la fonction citée ci-dessus. \begin{array}{lll} f:&\mathbb...
- 07 Juil 2019, 08:39
- Forum: ✯✎ Supérieur
- Sujet: image d'un réel
- Réponses: 21
- Vues: 1159
Re: Majorant
ah oui, il faut le comprendre ainsi :
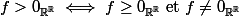
- 06 Juil 2019, 23:49
- Forum: ✯✎ Supérieur
- Sujet: Majorant
- Réponses: 8
- Vues: 506
Re: Majorant
J'ai supposé que ) ce sont donc les fonctions telles que
ce sont donc les fonctions telles que >0) et comparables ou les fonctions non comparables c'est à dire : les fonctions qui vérifient
et comparables ou les fonctions non comparables c'est à dire : les fonctions qui vérifient \in\R^2, \;f(x).f(y)<0)
- 06 Juil 2019, 08:45
- Forum: ✯✎ Supérieur
- Sujet: Majorant
- Réponses: 8
- Vues: 506
Re: Principe de récurrence
A\subset \N , et 0\in A \big(\forall n\in \N,\; n\in A\implies n+1\in A\big) \implies A=\N Pour le montrer on utilise le raisonnement par l'absurde, On suppose que \big(\forall n\in \N,\; n\in A\implies n+1\in A\big) \;\text{et}\; A\ne\N On considère l'ensemble \N\backslash A , de A...
- 06 Juil 2019, 00:00
- Forum: ✯✎ Supérieur
- Sujet: Principe de récurrence
- Réponses: 18
- Vues: 893
Re: Majorant
Bonsoir,
J'aurais proposé sans être affirmatif ceci:
\ge 0\big) \land \big(\exists x\in\R,\; f(x)>0\big)\bigg] \lor \bigg[\exists (x,y)\in\R^2, f(x)\cdot f(y)<0\bigg])
J'aurais proposé sans être affirmatif ceci:
- 05 Juil 2019, 22:36
- Forum: ✯✎ Supérieur
- Sujet: Majorant
- Réponses: 8
- Vues: 506
Re: Equivalence de deux fonctions
Note que
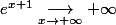
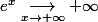
mais attention :
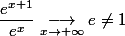
mais attention :
- 16 Déc 2018, 00:00
- Forum: ✯✎ Supérieur
- Sujet: Equivalence de deux fonctions
- Réponses: 13
- Vues: 975
- 10 résultats trouvés - Page 1 sur 1
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
