2) Comment puis-je calculer la fonction génératrice des moments ?
42 résultats trouvés
Revenir à la recherche avancée
Re: Loi de poisson composée
1) Je trouve = \int_{0}^{a}E(N| \lambda)f( \lambda) d\lambda = \frac{a}{2}) et
et = \frac{a^2}{12})
2) Comment puis-je calculer la fonction génératrice des moments ?
2) Comment puis-je calculer la fonction génératrice des moments ?
- 29 Nov 2020, 23:25
- Forum: ✯✎ Supérieur
- Sujet: Loi de poisson composée
- Réponses: 1
- Vues: 285
Loi de poisson composée
Bonjour, Soit une variable aléatoire N suit une loi de poisson composée. Le paramètre de la loi de poisson \lambda est donné par la variable aléatoire \gamma qui est une loi uniforme continue sur l'intervalle [0;a] (avec a>0). On rappelle que la densité de la fonction f est donnée par: f( \lambd...
- 27 Nov 2020, 20:23
- Forum: ✯✎ Supérieur
- Sujet: Loi de poisson composée
- Réponses: 1
- Vues: 285
Optimisation sous contrainte. Lagrange KKT
Bonjour, Soit (P) \max 2x_1+3x_2 \ sous les contraintes x^2_1+x^2_2 \leq 2 \ , \ x_1\geq 0 , \ x_2\geq 0 J'ai résolu le problème avec KKT et la dernière question est comment expliquer que l'on peut utiliser Lagrange pour résoudre ce problème . Pour utiliser Lagrange, il nous faut des contrai...
- 30 Jan 2020, 05:51
- Forum: ✯✎ Supérieur
- Sujet: Optimisation sous contrainte. Lagrange KKT
- Réponses: 5
- Vues: 511
Partie entière
Bonjour, Soit \tau >0 , quelque soit k \in \R , n_k=\lceil(1+ \tau)^k \rceil J'ai vu dans une correction que n_k=\lceil(1+ \tau)^k \rceil = \lfloor (1+\tau)^k \rfloor+1 ce qui me parait faux si (1+\tau)^k est un entier :? Quelle serait la relation exacte entre la part...
- 12 Déc 2019, 10:01
- Forum: ✯✎ Supérieur
- Sujet: Partie entière
- Réponses: 0
- Vues: 351
Re: Espérance
Merci pour vos réponses. @Yezu: 1) J'utilise le raisonnement sur la parité: \mathbb{E}[X^{2k+1}]=\int_{- \infty}^{0}{\frac{1}{\sqrt{2\pi}}x^{2k+1}e^{-\frac{1}{2}x^2}}dx+\int_{0}^{+\infty}{\frac{1}{\sqrt{2\pi}}x^{2k+1}e^{-\frac{1}{2}x^2}}dx x^{2k+1} est une fonction impaire et e^{-\frac{1}{2}x^2}} es...
- 06 Déc 2019, 05:54
- Forum: ✯✎ Supérieur
- Sujet: Espérance
- Réponses: 3
- Vues: 436
Espérance
Bonsoir, Soit X \sim \mathcal{N}(0,1) 1) Montrer que \forall k \in \mathbb{N}, \mathbb{E}[X^{2k+1}]=0 2) Montrer que \forall k \in \mathbb{N}, \mathbb{E}[X^{2k}]=\frac{(2k)!}{2^kk!} 1) k=0: \mathbb{E}[X^{2k+1}]=\mathbb{E}[X}]= 0 car X \sim \mathcal{N}(0,1) On suppose que c'es...
- 06 Déc 2019, 00:12
- Forum: ✯✎ Supérieur
- Sujet: Espérance
- Réponses: 3
- Vues: 436
Re: Espérance conditionnelle
Je prends alors 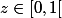 ?
?
- 25 Juin 2019, 00:12
- Forum: ✯✎ Supérieur
- Sujet: Espérance conditionnelle
- Réponses: 9
- Vues: 524
Re: Espérance conditionnelle
Je divise donc en 2 lorsque X-1 est négatif et X-1 positif: -\int_{0}^{1}{\psi (Z)(-(\sqrt{Z}+1)-\phi(Z)) \frac{-dz}{6\sqrt{z}}+\int_{1}^{4}{\psi (Z)(\sqrt{Z}+1-\phi(Z)) \frac{dz}{6\sqrt{z}}=0} \int_{0}^{1}{\psi (Z)(-(\sqrt{Z}+1...
- 24 Juin 2019, 20:31
- Forum: ✯✎ Supérieur
- Sujet: Espérance conditionnelle
- Réponses: 9
- Vues: 524
Re: Espérance conditionnelle
4) si X et Y sont indépendants, alors 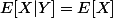 mais je ne vois pas comment l'utiliser avec la fonction.
mais je ne vois pas comment l'utiliser avec la fonction.
- 24 Juin 2019, 19:30
- Forum: ✯✎ Supérieur
- Sujet: Espérance conditionnelle
- Réponses: 9
- Vues: 524
Re: Espérance conditionnelle
1) E[X|Z]=\phi(Z) \\ \forall \psi(Z) \ E[\psi (Z)(X-\phi(Z))]=0 \\ E[\psi (X^2-2X+1)(X-\phi(X^2-2X+1))]=0 \\ \int_{0}^{3}{\psi (X^2-2X+1)(X-\phi(X^2-2X+1)) \frac{dx}{3}=0} chgt de variable: Z=(X-1)^2, \ X...
- 24 Juin 2019, 19:05
- Forum: ✯✎ Supérieur
- Sujet: Espérance conditionnelle
- Réponses: 9
- Vues: 524
Espérance conditionnelle
Bonjour, Soit X,Y deux variables aléatoire indépendantes uniformément distribués sur [0,3] et soit Z=(X-1)^2 1) Calculer E[X|Z] 2) Calculer E[Z|X] 3) Calculer E[Y|Z] 4) Prouver que pour toute fonction f mesurable bornée : E[f(X)|Y,Z]=E[f(X)|Z] 2) E[Z|X]= Z 3) E[Y|Z] = E[Y]=\f...
- 24 Juin 2019, 18:13
- Forum: ✯✎ Supérieur
- Sujet: Espérance conditionnelle
- Réponses: 9
- Vues: 524
Re: Calcul inf sup
Oui merci , grosse erreur de ma part , j'ai pris ) au lieu de
au lieu de )

Merci beaucoup pour l'aide que vous m'avez apporté

Merci beaucoup pour l'aide que vous m'avez apporté
- 09 Mar 2019, 14:27
- Forum: ✯✎ Supérieur
- Sujet: Calcul inf sup
- Réponses: 13
- Vues: 604
Re: Calcul inf sup
@Tournesol : Merci j'ai enfin compris :) J'aimerais également avoir de l'aide sur les expressions suivantes: 1) f(x,y)=(x-5)y , X= \R , Y=[- \infty , 0] 2) g(x,y)=x^2y , X= \R^+_* , Y= \R 3) h(x,y)= |x-y+5| , X=Y= \R 4) i(x,y)= |x-y+5|, X= [2,10[, Y=[3,9] 1) \...
- 09 Mar 2019, 06:08
- Forum: ✯✎ Supérieur
- Sujet: Calcul inf sup
- Réponses: 13
- Vues: 604
Re: Calcul inf sup
@Aviateur: 5) b)Merci, je trouve bien que les 2 paraboles se croisent en y=1 donc 4 3)a)-infini b)0 . Ok c'est bon j'ai compris merci :) @Tournesol : Merci pour vos réponses. Pour 1)a) Si j'ai bien compris, numérateur >0 et on prend y qui tend vers -1 avec y<-1 pour avoir -infini , c'est bien ça ? ...
- 08 Mar 2019, 19:33
- Forum: ✯✎ Supérieur
- Sujet: Calcul inf sup
- Réponses: 13
- Vues: 604
Re: Calcul inf sup
Merci pour votre réponse Voici comment j'ai raisonné: 1)b) Pourquoi Y= \R - 0 et pas \R - \{-1\} ? \varphi(y)= sup_x \frac{x-5}{y+1}= \left\lbrace\begin{matrix} + \infty & si \ y>-1 \\ 0 & si \ y<-1 \end{matrix}\right. \Rightarrow inf_y \varphi(y) = 0 2) \varphi(x)= i...
- 08 Mar 2019, 02:22
- Forum: ✯✎ Supérieur
- Sujet: Calcul inf sup
- Réponses: 13
- Vues: 604
Calcul inf sup
Bonsoir, Je dois trouver le sup_x inf_y \ et \ inf_y sup_x de ces expressions: 1)a(x,y)= \frac{x-5}{y+1} ,X=]5, +\infty[, Y= \R - 0 \\ 2) b(x,y)=\frac{xy}{y-5}, X=Y=[-1,5[ \\ 3) c(x,y)= \frac{xy}{y-5}, X=Y=]0,5[ \\ 4) d(x,y)= (y-1-x)^2, X=Y= \R...
- 07 Mar 2019, 23:28
- Forum: ✯✎ Supérieur
- Sujet: Calcul inf sup
- Réponses: 13
- Vues: 604
Re: Probabilités
Oui pour calculer la densité de U et V j'ai utilisé les fonctions de répartition mais je vais aussi m'entraîner avec cette nouvelle méthode.
Je tiens à vous remercier pour le temps et les explications détaillé que vous m'avez apporté sur l'ensemble de l'exercice
Je tiens à vous remercier pour le temps et les explications détaillé que vous m'avez apporté sur l'ensemble de l'exercice
- 27 Juin 2018, 00:05
- Forum: ✯✎ Supérieur
- Sujet: Probabilités
- Réponses: 38
- Vues: 1401
Re: Probabilités
Merci pour l'intuition, j'ai pu comprendre. Par contre j'ai vraiment du mal à le montrer mathématiquement. Je ne sais pas si ce que j'ai fait précédemment est bon, mais si on les additionne je ne vois pas ce que ce que cela donnera à cause du changement de var. Cette exercice me dépasse un peu, j'ai...
- 25 Juin 2018, 00:30
- Forum: ✯✎ Supérieur
- Sujet: Probabilités
- Réponses: 38
- Vues: 1401
Re: Probabilités
Je ne suis pas sur d'avoir bien compris ce qu'il fallait calculer. E[1_{X<Y}h(X,Y) ]= \int_{\R^2} 1_{X<Y} h(x,y) f_{(X,Y)}(x,y)dxdy = \int_{\R^2}1_{X<Y} h(x,y) e^{-x-y} dxdy \\ E[1_{X'<Y'}h(X',Y') ]= \int_{\R^2} 1_{X'<Y'} h(...
- 24 Juin 2018, 23:14
- Forum: ✯✎ Supérieur
- Sujet: Probabilités
- Réponses: 38
- Vues: 1401
Re: Probabilités

- 24 Juin 2018, 22:43
- Forum: ✯✎ Supérieur
- Sujet: Probabilités
- Réponses: 38
- Vues: 1401
- 42 résultats trouvés - Page 1 sur 3 • 1, 2, 3
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
