Forum de Mathématiques: Maths-Forum

la factorisation a peu d'importance f'(x)=b(e^{-x})+(bx)(-e^{-x})=b(1-x)e^{-x} f'(0)=b donc b=1 merci j'ai compris du coup! PS: oui je flood en créant 5 topics par jour mais je suis en galère j'ai un concours demain et jeudi.. :( Ne t'inquiète pas pour ça...

pascal16 a écrit:que trouves-tu pour f'(x) ?
ça te donne quoi comme équation f'(0)=1

j'ai calculé f'(x), mais je n'arrive pas à factoriser l'expression obtenue:

j'obtiens

edit: je pense avoir trouvé!
ah non en fait toujours bloqué..

Bonjour/bonsoir, on donne f(x)=a+bxe^{-x} f passe par le points de coordonnées (0;1) et admet en ce point une tangente de pente 1. démontrer que a = b = 1 par énoncé, j'en ai déduit que: f(0)=1 et que f'(0)=1 j'ai ensuite calculé f(0) et j'ai trouvé 1. Donc a=1 Le problème, c'est que je n'ai...

Evidemment ! Mais si on te pose la question c'est qu'en général elle a une solution.... qui est assez évidente. Ici 1 car on sait que ln 1 =0... si c'est trop compliqué la valeur qui annule est donnée dans l'énoncé ou alors on en trouve une valeur approchée, la valeur exacte etant notée alpha par e...

En effet, mais on se sert très souvent du sens de variation pour trouver le signe. Par exemple, si g est strictement croissante sur ]0;+inf[ et que g(3)=0 Alors pour tout réel x supérieur à 3, on a x> ou = 3 donc g(x) > ou = g(3) c'est à dire g(x)> ou =0, donc g(x) positif Inversement si x est infé...

Bonjour, Non on ne peut pas isoler x, pour trouver le signe, méthode classique, dérivée tableau de variation sur lequel on indiquera g(1) et on peut alors conclure. mais en calculant la dérivée g' et en étudiant son signe, on a le sens de variation de g, pas son signe.. :/ edit: j'ai étudié le sign...

Bonjour à tous, une fois n'est pas coutume, je me retrouve bloqué face à une question: soit g(x)=x-1+ln(x) Montrer que g est positive sur [1;+\propto [ Justifier J'ai essayé de résoudre l'inéquation g(x)>0 ,mais je me retrouve bloqué par un x que je n'arrive pas à simplifier....

salut, merci pour ton aide!

donc si j'ai bien compris, 2ln(x)+1 est de signe négatif pour x<=exp(-1/2)?

(pour des fonctions plus usuelles je ne me serais pas posé la question question mais là)

Bonjour, voici l'énoncé: Soit f(x)=ln^2(x)+ln(x) Démontrer que \frac{1}{4} est le minimum de f sur ]0;+\propto [ J'ai calculé la dérivée f' de f, et j'obtiens: f'(x)=\frac{2lnx+1}{x} Je constate que f'(x)=0 pour x=e^{-\frac{1}{2}}=\frac{1}{\sqrt{e}} J'...

pascal16 a écrit:regarde ma réponse, j'ai levé les les problèmes et la solution coule de source, c'est 1 la limite.

on a

effectivement, la limite est 1. merci!

Ben... le principe était pas bon : c'était pas une erreur mais bien un truc volontaire : Pour montrer que ton truc tend pas vers 0, c'est pas la peine de s'emmerder : il est clairement tout le temps supérieur à 1 et ça suffit (largement) à montrer qu'il tend pas vers 0. N'empêche qu'à titre d'exerc...

\frac{1}{x}+\frac{\sqrt{1+x^2}}{x} à \frac{1}{x}+\frac{\sqrt{x^2}}{x} Il veut dire quoi l'espèce de symbole que zygo a mis entre ces deux expressions ? "supérieur à", j'étais parti du principe qu'il s'agissait d'une erreur, et qu'en fait c'était un "=" Edit: Autant pour moi j'ai...

Merci à vous deux, mais j'aurais besoin d'une petite précision...

par quelle opération passe-t-on de
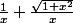à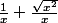
où est donc passé le 1 sous la racine?
désolé quand je vous dis que j'ai des lacunes...

(Re)bonjour, bonsoir toujours dans ma préparation du concours acces, je commence à prendre mes repères, mais je me retrouve à nouveau bloqué.. Voici l'énoncé: Soit f(x)=\frac{1+\sqrt({1+x^2)}}{x} L'affirmation suivante est-elle vraie ou fausse? \lim_{x\rightarrow +\propto }=0 Je me d...

d'accord merci!

merci je comprends déjà mieux.

vous avez raison vous m'avez déjà bien aidé, la seule option qui s'offre à moi c'est le travail.

Merci encore.

est-ce qu'il est possible d'utiliser la "méthode de l'hospital"? càd que si lim (f(x)) = g(x)/h(x) = inf/inf ou 0/0 (forme indéterminée) cela équivaut à lim(f(x))= g'(x)/h'(x) x => a est-ce correct? Parce qu'il se trouve que j'ai des lacunes concernant les calculs impliquant des racines, q...

Merci beaucoup pour votre aide.

Le programme de maths en ES n'aborde que très peu la notion de limite, par ailleurs j'ai commis l'erreur de m'y mettre un peu tard au niveau révisions...

Bonne journée

Bonjour, je suis actuellement en train de préparer mon épreuve de math du concours acces, et je bloque sur une question. Il s'agit de calculer la limite (en +inf) suivante: lim (sqrt((x-1)/(x+1))) x=>+inf La racine n'est pas un problème en soi, c'est après où je suis perdu. Le corrigé indique que ce...