Déterminer le sens de variation de f

[pie]

Bonjour,
voici l'énoncé:

Soit

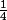
Démontrer que est le minimum de f sur

J'ai calculé la dérivée f' de f, et j'obtiens:



Je constate que pour

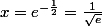
J'ai dressé un tableau de signes mais je bloque sur l'étude du signe de 2ln(x)+1...
merci pour votre aide (et votre soutien)

[Lostounet]

Salut Pie!

Il suffit de résoudre:
2ln(x)+1 >= 0

Cela marche comme suit:

2ln(x)>= -1

Ln(x)>=-1/2

Or la fonction exponentielle est croissante sur R (donc elle conserve le sens des inégalités):

Exp(ln(x)) >= exp(-1/2)
X>=exp(-1/2)

Courage... et bienvenue sur Maths forum

[pie]

salut, merci pour ton aide!

donc si j'ai bien compris, 2ln(x)+1 est de signe négatif pour x<=exp(-1/2)?

(pour des fonctions plus usuelles je ne me serais pas posé la question question mais là)

[pascal16]

Vu que as déjà là où elle s'annule, calculer tout simplement une valeur entre deux racines te donne le signe. Confirme tes résultats par un tracé à la calculette, sous géogebra ou graph.tk

[zygomatique]

salut

la fonction x --> 2 ln x + 1 est trivialement strictement croissante ... donc si on sait où elle s'annule on connait son signe ...

[Black Jack]

f(x) = ln²(x) + ln(x) = (ln(x) + 1/2)² - 1/4 (sur ]0 ; +oo[)

Comme (ln(x) + 1/2)² >= 0 (puisque c'est un carré), f est min pour (ln(x) + 1/2) = 0 et ce min est -1/4