Problème limite d'un quotient
17 messages
- Page 1 sur 1
problème limite d'un quotient
Bonjour,
je suis actuellement en train de préparer mon épreuve de math du concours acces, et je bloque sur une question.
Il s'agit de calculer la limite (en +inf) suivante:
lim (sqrt((x-1)/(x+1)))
x=>+inf
La racine n'est pas un problème en soi, c'est après où je suis perdu.
Le corrigé indique que cette limite fait 1, mais je trouve inf/inf, qui pour moi est une forme indéterminée..
Merci pour votre aide!
je suis actuellement en train de préparer mon épreuve de math du concours acces, et je bloque sur une question.
Il s'agit de calculer la limite (en +inf) suivante:
lim (sqrt((x-1)/(x+1)))
x=>+inf
La racine n'est pas un problème en soi, c'est après où je suis perdu.
Le corrigé indique que cette limite fait 1, mais je trouve inf/inf, qui pour moi est une forme indéterminée..
Merci pour votre aide!
Re: problème limite d'un quotient
Salut,
Mettre en facteur par au numérateur et au dénominateur, ils s'annulent et il reste quand x tend vers
au numérateur et au dénominateur, ils s'annulent et il reste quand x tend vers  au final
au final  soit
soit 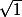 ,
,
d'ailleurs :

Mettre en facteur par
d'ailleurs :

Modifié en dernier par laetidom le 02 Avr 2017, 11:47, modifié 4 fois.
Re: problème limite d'un quotient
Salut,
LE truc qu'il faudrait quand même comprendre, c'est que, face à la question "combien vaut la limite de truc", de répondre "c'est une forme indéterminé", c'est totalement exactement la même chose que de répondre "j'en sais rien", ni plus, ni moins.
Donc, là, toi tu affirme que tu en sait rien alors que le corrigé, lui il affirme qu'il sait et que ça vaut 1.
Et il n'y a bien sûr pas la moindre contradiction entre les deux affirmations.
Ensuite,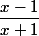 , lorsque
, lorsque  est non nul et différent de -1, c'est égal à
est non nul et différent de -1, c'est égal à  (en divisant le numérateur et le dénominateur par "ce qui semble le plus important", à savoir
(en divisant le numérateur et le dénominateur par "ce qui semble le plus important", à savoir  )
)
Ben, c'est absolument pas contradictoire l'un avec l'autre...pie a écrit:Le corrigé indique que cette limite fait 1, mais je trouve inf/inf, qui pour moi est une forme indéterminée..
LE truc qu'il faudrait quand même comprendre, c'est que, face à la question "combien vaut la limite de truc", de répondre "c'est une forme indéterminé", c'est totalement exactement la même chose que de répondre "j'en sais rien", ni plus, ni moins.
Donc, là, toi tu affirme que tu en sait rien alors que le corrigé, lui il affirme qu'il sait et que ça vaut 1.
Et il n'y a bien sûr pas la moindre contradiction entre les deux affirmations.
Ensuite,
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: problème limite d'un quotient
Merci beaucoup pour votre aide.
Le programme de maths en ES n'aborde que très peu la notion de limite, par ailleurs j'ai commis l'erreur de m'y mettre un peu tard au niveau révisions...
Bonne journée
Le programme de maths en ES n'aborde que très peu la notion de limite, par ailleurs j'ai commis l'erreur de m'y mettre un peu tard au niveau révisions...
Bonne journée
Re: problème limite d'un quotient
Pas de soucis, l'important est de prendre conscience positivement des choses et d'essayer de faire au mieux . . .
Bonne journée, @+ sur le forum.
Bonne journée, @+ sur le forum.
Re: problème limite d'un quotient
salut
(x - 1)/(x + 1) = 1 - 2/(x + 1)
...
(x - 1)/(x + 1) = 1 - 2/(x + 1)
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: problème limite d'un quotient
zygomatique a écrit:salut
(x - 1)/(x + 1) = 1 - 2/(x + 1)
...
. . . et oui, effectivement en faisant la division euclidienne de
Re: problème limite d'un quotient
est-ce qu'il est possible d'utiliser la "méthode de l'hospital"?
càd que si lim (f(x)) = g(x)/h(x) = inf/inf ou 0/0 (forme indéterminée)
cela équivaut à lim(f(x))= g'(x)/h'(x)
x => a
est-ce correct? Parce qu'il se trouve que j'ai des lacunes concernant les calculs impliquant des racines, quotients, etc...
J'aimerais trouver une méthode fiable pour calculer une limite s'il en existe une..
càd que si lim (f(x)) = g(x)/h(x) = inf/inf ou 0/0 (forme indéterminée)
cela équivaut à lim(f(x))= g'(x)/h'(x)
x => a
est-ce correct? Parce qu'il se trouve que j'ai des lacunes concernant les calculs impliquant des racines, quotients, etc...
J'aimerais trouver une méthode fiable pour calculer une limite s'il en existe une..

Re: problème limite d'un quotient
pie a écrit:. . . j'ai des lacunes concernant les calculs impliquant des racines, quotients, etc...
Une petite aide supplémentaire :

Re: problème limite d'un quotient
pie a écrit:est-ce qu'il est possible d'utiliser la "méthode de l'hospital"?
J'aimerais trouver une méthode fiable pour calculer une limite s'il en existe une..
un peu de sérieux pas besoin d'un bulldozer pour planter une fleur !!!
ben314 et moi-même t'avons donné deux méthodes classiques ...
x - 1 = x + 1 - 2 et il suffit de diviser par x + 1 ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: problème limite d'un quotient
merci je comprends déjà mieux.
vous avez raison vous m'avez déjà bien aidé, la seule option qui s'offre à moi c'est le travail.
Merci encore.
vous avez raison vous m'avez déjà bien aidé, la seule option qui s'offre à moi c'est le travail.
Merci encore.
Re: problème limite d'un quotient
pie a écrit:merci je comprends déjà mieux. ===> superbe !!
vous avez raison vous m'avez déjà bien aidé, la seule option qui s'offre à moi c'est le travail. ===> Bon courage.
Merci encore.
On n'est pas loin si il faut.
Re: problème limite d'un quotient
pie a écrit:est-ce qu'il est possible d'utiliser la "méthode de l'hospital"?
càd que si lim (f(x)) = g(x)/h(x) = inf/inf ou 0/0 (forme indéterminée)
cela équivaut à lim(f(x))= g'(x)/h'(x)
x => a
est-ce correct? Parce qu'il se trouve que j'ai des lacunes concernant les calculs impliquant des racines, quotients, etc...
J'aimerais trouver une méthode fiable pour calculer une limite s'il en existe une..
Oui tu peux utiliser cette méthode mais ... vaut mieux le faire uniquement en dernier recours !
Souvent une mise en facteur du terme dominant permet de s'en sortir rapidement.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: problème limite d'un quotient
Lostounet a écrit:pie a écrit:est-ce qu'il est possible d'utiliser la "méthode de l'hospital"?
càd que si lim (f(x)) = g(x)/h(x) = inf/inf ou 0/0 (forme indéterminée)
cela équivaut à lim(f(x))= g'(x)/h'(x)
x => a
est-ce correct? Parce qu'il se trouve que j'ai des lacunes concernant les calculs impliquant des racines, quotients, etc...
J'aimerais trouver une méthode fiable pour calculer une limite s'il en existe une..
Oui tu peux utiliser cette méthode mais ... vaut mieux le faire uniquement en dernier recours !
Souvent une mise en facteur du terme dominant permet de s'en sortir rapidement.
on est en terminale ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: problème limite d'un quotient
perso, je l'avais fait en term.
si f et g tendent vers 0 touts les deux f/g tend vers}/g^{(n)}) où n désigne le premier orde dérivée non nulle de l'une des deux fonctions
où n désigne le premier orde dérivée non nulle de l'une des deux fonctions
J'ai regardé le programme officiel, on doit faire la théorie, mais pas trop et pour des problèmes de niveau terminal (ça donne une définition circulaire).
si f et g tendent vers 0 touts les deux f/g tend vers
J'ai regardé le programme officiel, on doit faire la théorie, mais pas trop et pour des problèmes de niveau terminal (ça donne une définition circulaire).
Re: problème limite d'un quotient
A mon sens, y'a aussi (voir surtout) le problème que, hélas, les "bêtes calculs algébriques", le moins qu'on puisse dire, c'est que c'est plus du tout maitrisé par le "terminale de base" et que les calculs de limites "à la main", ben c'est quand même l'occasion d'en repasser une (n+1)-ième couche en ce qui concerne les règles de calculs (factorisations, développement, simplifications de fractions, racines carrées, etc...)
Sans parler du fait que ça oblige un minimum à "comprendre" une formule : chercher le(s) terme(s) "dominant" et ceux "qui ne servent à rien" et comment "changer de forme" une expression.
Sans parler du fait que ça oblige un minimum à "comprendre" une formule : chercher le(s) terme(s) "dominant" et ceux "qui ne servent à rien" et comment "changer de forme" une expression.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
