Forum de Mathématiques: Maths-Forum

Bonsoir, il y a quelque chose que je ne comprends pas bien On prend A une matrice à coefficients entiers relatifs tels que il existe k in\mathbb{N} tel que A^{k} = In . Cependant j'ai lu dans une correction d'un exercice que A était diagonalisable et ce sans aucune explication. On n'a pas d'autres i...

Il n'y a pas de lien
Je pense qu'aussi la philosophie de ce forum est de poster son énoncé, expliquer ce qui a déjà été fait, dire ou on coince et ensuite on pourra te venir en aide

Bonjour, je ne vois pas du tout comment paramétrer une courbe à partir d'une équation comme celle-ci x^2 + xy - y^2 + 3x + 2y = 1 Après avoir cherché sur le net, dans beaucoup de cas il est posé y = tx sans trop d'explications, cependant je ne comprends pas d'ou cela vient, et j'ai l'impression que ...

Bonjour je bug sur un énoncé:
On a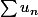 une série divergente et il faut donner un exemple ou la série 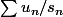est divergente avec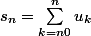
Cependant je ne vois pas du tout, je pensais d'abord à la série harmonique
Merci de votre aide

Je pense deja qu'il y a une erreur d'énoncé ici

Sharkk a écrit:Le principe consiste à générer la liste nombres entre 1 et n qui sont sommes de k puissances
n-ièmes

Ce serait plus rechercher à générer les nombres de 1 à N

Bonjour, voila j'ai un petit soucis avec un problème en python qui est le suivant: Deux entiers n,N > 1 étant donnés, écrire un programme python déterminant le plus petit entier w(n,N) entre 1 et N nécessitant le plus de puissances n-ièmes dans sa décomposition de longueur minimale en somme de puiss...

L'énoncé précis est Soit T l application de R dans R qui à fait fait correspondre T(f) définie par (T(f))(x) = f(x+1)

Merci de votre réponse et désolé de l imprécision On sait juste que T est une application de R dans R Excusez moi aussi j ai mal formule la question On ne demande pas de déduire l injectivite mais plutôt que peut on déduire de l injectivite T - a Id J imaginais donc qu elle le n était pas si on posa...

Bonjour, je bloque sur l'énoncé de quelque chose: On défini une application T telle que T(f) = f(x+1) A une question, on me demande de trouver une fonction f telle que T(f) = a*f Je trouve par exemple: f(x) = e^{x*ln(a)} Puis on me demande d'en déduire l'injec...

Merci de ta réponse, j'ai déjà effectué ceci !! je trouve un DL a l'ordre 3 qui est:


Mais je bloque ici

Bonjour, j'essaie de montrer que la fonction: f(x) = \frac{1}{ln(1+x)} - \frac{1}{x} possède un développement limité à l'ordre n en 0, mais on a jamais fait ça en cours et je ne vois pas du tout comment faire. Peut-etre montrer que la fonction est dérivable n fois en 0? mais je n'y a...

Merci beaucoup de ton aide,
Bonne journée

Merci de ta réponse, effectivement ça serait plus joli mais ducoup je ne peux plus appliquer les fonctions symétriques puisque mon polynome n'est pas unitaire (Coefficient du terme de plus haut degré égal à 1) et effectivement je n'ai pas de racines évidentes, et c'est la première fois que j'arrive ...

Bonjour je suis amené à résoudre l'équation complexe suivante : x^{3} - (\frac{14}{5} \times i + \frac {7}{5} ) \times x^{2} +(4 \times i + 1) \times x - (\frac {6}{5} \times i - \frac {3}{5}) = 0 *Oui ma première équation en TeX* voila en classe nous avions toujours une rela...

Merci beaucoup de ta réponse, c'est pas la première fois que tu m'aides il me semble!! Donc merci vraiment
Je vais de ce pas voir le tutoriel "MimeTeX" merci

Bonne journée

Bonjour, Je bloque sur quelque chose surement de très bête, cependant je ne comprends pas la décomposition: 1/(X**n -1) Je comprends que c'est la somme de 0 à n-1 des ak/(X - e** (i2kpi / n)) mais seulement je ne comprends pas pourquoi ak = 1/n * e**(2ikpi/n) Merci d'avance, Désole si ce n'est pas t...

Merci beaucoup pour votre aide )

Bonjour, je bloque sur une question Soit une urne qui contient n boules distinctes numérotées 1;2;3;.....;n on effectue un tirage de p boules Dans le cadre de tirages successifs et avec remise, je dois démontrer que le nombre de tirages possibles pour lesquels la somme des numéros tirés est p + 2 es...

Voila, je bloque la justement!!
Non nous n'avons pas appris , ou du moins pas encore !

exp(2z) excuse moi pour l'imprécision