Bonsoir,
J'aimerai savoir comment on peut calculer l'exposant de Liapunov pour les systèmes dynamiques, par exemple pour le système de Lorenz.
Merci infiniment
57 résultats trouvés
Revenir à la recherche avancée
- 03 Oct 2021, 16:07
- Forum: ✯✎ Supérieur
- Sujet: Système dynamique
- Réponses: 0
- Vues: 333
Re: système de lorenz
Merci pour la réponse,alors est-ce que je dois changer les conditions initiales pour obtenir la structure de l'attracteur de lorenz?
Merci encore
Merci encore
- 19 Avr 2021, 07:23
- Forum: ✯✎ Supérieur
- Sujet: système de lorenz
- Réponses: 2
- Vues: 287
système de lorenz
Bonsoir,
J'essaye d'intégrer le système d'équations différentielles de l'attracteur de lorenz.En utilisant les conditions initiales x(0)=y(0)=z(0)=0,je ne comprends pas pourquoi je trouve des solutions toutes égales à zero.Est-ce normal?
Merci d'avance
J'essaye d'intégrer le système d'équations différentielles de l'attracteur de lorenz.En utilisant les conditions initiales x(0)=y(0)=z(0)=0,je ne comprends pas pourquoi je trouve des solutions toutes égales à zero.Est-ce normal?
Merci d'avance
- 18 Avr 2021, 18:36
- Forum: ✯✎ Supérieur
- Sujet: système de lorenz
- Réponses: 2
- Vues: 287
Re: Crochet de Lie
D'accord je vois,merci beaucoup!
- 05 Oct 2020, 19:15
- Forum: ✯✎ Supérieur
- Sujet: Crochet de Lie
- Réponses: 2
- Vues: 512
Crochet de Lie
Bonjour,
Comment est-ce qu'on montre qu'un crochet est bien un crochet de Lie?
Merci d'avance
Comment est-ce qu'on montre qu'un crochet est bien un crochet de Lie?
Merci d'avance
- 01 Oct 2020, 09:35
- Forum: ✯✎ Supérieur
- Sujet: Crochet de Lie
- Réponses: 2
- Vues: 512
Symboles de Christoffel
Bonjour,
J'aimerai savoir comment on reconnait si un symbole de Christoffel de première espèce est nul pour une métrique donnée
Merci infiniment
J'aimerai savoir comment on reconnait si un symbole de Christoffel de première espèce est nul pour une métrique donnée
Merci infiniment
- 17 Mar 2020, 08:08
- Forum: ✯✎ Supérieur
- Sujet: Symboles de Christoffel
- Réponses: 1
- Vues: 526
Inégalité de Hölder
Bonjour, Comment parvenir à cette inégalité \sum_{i=1}^{N}{u_iv_i}\leq \left( \sum_{i=1}^{N}{(u^p_i)}\right)^{1/p}\left( \sum_{i=1}^{N}{(v^q_i)}\right)^{1/q} à partir de \sum_{i=1}^{N}{\frac{x_iy_i}{||x||_p||y||_q}}\leq \frac{1}{p}\left( \sum_{i=1}^{N}{\frac{x^p_i...
- 14 Mar 2020, 14:17
- Forum: ✯✎ Supérieur
- Sujet: Inégalité de Hölder
- Réponses: 0
- Vues: 353
Transformée de Fourier
Bonjour,
Voici mon énoncé:
Soit la fonction=e^{-|t|}sin(t)) .Trouver la tranformée de Fourier de f(t).
.Trouver la tranformée de Fourier de f(t).
Je fais une intégration par parties mais après quelles bornes doit-je prendre pour calculer F(t)?
Merci d'avance
Voici mon énoncé:
Soit la fonction
Je fais une intégration par parties mais après quelles bornes doit-je prendre pour calculer F(t)?
Merci d'avance
- 07 Sep 2019, 12:33
- Forum: ✯✎ Supérieur
- Sujet: Transformée de Fourier
- Réponses: 0
- Vues: 305
Fonction géneratrice d'une variable
Bonjour,
J'aimerai savoir comment on fait pour trouver la fonction generatrice d'une variable aléatoire X si on connait par exemple sa densité de probabilité
Merci d'avance
J'aimerai savoir comment on fait pour trouver la fonction generatrice d'une variable aléatoire X si on connait par exemple sa densité de probabilité
Merci d'avance
- 17 Juil 2018, 10:45
- Forum: ✯✎ Supérieur
- Sujet: Fonction géneratrice d'une variable
- Réponses: 1
- Vues: 266
Re: Abscisse curviligne
Bonjour,
Est-ce que les coordonnées de A interviennent dans le calcul de s(t)?
Merci d'avance
Est-ce que les coordonnées de A interviennent dans le calcul de s(t)?
Merci d'avance
- 12 Fév 2018, 03:38
- Forum: ✯✎ Supérieur
- Sujet: Abscisse curviligne
- Réponses: 5
- Vues: 1209
Re: Abscisse curviligne
Bonsoir,
L'abcisse curviligne est=\int_{to}^{t1}{\parallel\vec{M'(t)\parallel }dt)
N'a-t-on pas besoin des coordonnées de A pour calculer s(t1) du point B?
L'abcisse curviligne est
N'a-t-on pas besoin des coordonnées de A pour calculer s(t1) du point B?
- 11 Fév 2018, 21:32
- Forum: ✯✎ Supérieur
- Sujet: Abscisse curviligne
- Réponses: 5
- Vues: 1209
Abscisse curviligne
Bonsoir,
Comment calculer l'abscisse curviligne d'un point de paramètre t1 d 'une courbe dans R^3 si on choisit un point A de paramètre t' par exemple comme origine et qu'on conmait le paramétrage de la courbe?
Merci infiniment
Comment calculer l'abscisse curviligne d'un point de paramètre t1 d 'une courbe dans R^3 si on choisit un point A de paramètre t' par exemple comme origine et qu'on conmait le paramétrage de la courbe?
Merci infiniment
- 11 Fév 2018, 20:50
- Forum: ✯✎ Supérieur
- Sujet: Abscisse curviligne
- Réponses: 5
- Vues: 1209
Re: Aire d'une surface dans R^2
Bonjour,
M'(u)=(1,2u,v);M'(v)=(2,-2v,u) ,M'(u)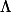 M'(v)=(2 u^2 + 2 v^2;2v-u;-2v-4u) ;la norme donne un truc très long puissance 1/2 donc je ne sais pas trop et pour le domaine c'est R^2 donc je ne vois comment intégrer..
M'(v)=(2 u^2 + 2 v^2;2v-u;-2v-4u) ;la norme donne un truc très long puissance 1/2 donc je ne sais pas trop et pour le domaine c'est R^2 donc je ne vois comment intégrer..
Cordialement
M'(u)=(1,2u,v);M'(v)=(2,-2v,u) ,M'(u)
Cordialement
- 13 Jan 2018, 16:10
- Forum: ✯✎ Supérieur
- Sujet: Aire d'une surface dans R^2
- Réponses: 8
- Vues: 860
Re: Aire d'une surface dans R^2
Bonjour,
Je m'excuse vraiment pour le multi post mais j'aurai vraiment besoin votre aide..
Merci infiniment
Je m'excuse vraiment pour le multi post mais j'aurai vraiment besoin votre aide..
Merci infiniment
- 13 Jan 2018, 12:31
- Forum: ✯✎ Supérieur
- Sujet: Aire d'une surface dans R^2
- Réponses: 8
- Vues: 860
Re: Aire d'une surface dans R^2
Mais alors je ne comprends pas pourquoi avec le théorème Q'x-P'y,on n'obtient pas 0,la courbe n'est donc pas fermée?? Et que faire si on donne le paramétrage de (S): \begin{cases} & \ x= u+2v\\ & \ y=u^3-v^2 \\ & \ z= uv+5 \end{cases} je ne vois pas comment obtenir le résultat avec le (1...
- 13 Jan 2018, 12:05
- Forum: ✯✎ Supérieur
- Sujet: Aire d'une surface dans R^2
- Réponses: 8
- Vues: 860
Aire d'une surface dans R^2
Bonjour, Voici mon problème...: Soit (C)une courbe dans R^2 entourant une surface (S) Montrer que l'aire de (S)= \int_{(C)}^{}{\frac{1}{2}(x dy-y dx)} En déduire l'aire de l'ellipse \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 ;ab\neq 0 Pouvez-vous m'indiquer comment faire je vous en supplie......
- 13 Jan 2018, 05:11
- Forum: ✯✎ Supérieur
- Sujet: Aire d'une surface dans R^2
- Réponses: 8
- Vues: 860
solubilité et concentration
Bonjour, Dans cet exercice je ne comprends pas pourquoi je trouve des valeurs différentes sur la concentration??: La solubilité du CaSO4 est de 4,90.10^(-3)mol.L^(-1).On introduit 500mg de CaSO4 dans 1L d'eau; 1)Quelle est la concentration molaire des ions Ca^(2+) et SO4^(2-) dans la solution? 2)le ...
- 27 Déc 2017, 02:23
- Forum: ☣ Chimie
- Sujet: solubilité et concentration
- Réponses: 1
- Vues: 1237
Re: Changement de repère
Merci encore pour l'explication!Maintenant on me demande de déterminer les angles d'Euler,mais là je ne sais pas s'il s'agit juste de mentionner ou bien de tous les exprimer en fonction de X,Y,Z et si c'est cela comment doit-on faire?
- 09 Sep 2017, 19:14
- Forum: ✯✎ Supérieur
- Sujet: Changement de repère
- Réponses: 8
- Vues: 587
Re: Changement de repère
Merci encore pour votre réponse!Mais dans les expressions ils y a quand même des racines d'après ce que j'ai fait :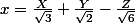 et
et }{\sqrt{3}};Y=\frac{x+z}{\sqrt{2}};Z=\frac{-(x+2y-z)}{\sqrt{6}})
- 09 Sep 2017, 14:14
- Forum: ✯✎ Supérieur
- Sujet: Changement de repère
- Réponses: 8
- Vues: 587
Re: Changement de repère
Bonjour,
Je ne vois pas comment trouver x,y,z?
J'ai trouvé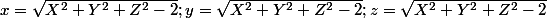 ,mais cela donne toujours 0 avec le phi
,mais cela donne toujours 0 avec le phi
Je ne vois pas comment trouver x,y,z?
J'ai trouvé
- 09 Sep 2017, 08:06
- Forum: ✯✎ Supérieur
- Sujet: Changement de repère
- Réponses: 8
- Vues: 587
- 57 résultats trouvés - Page 1 sur 3 • 1, 2, 3
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
