28 résultats trouvés
Revenir à la recherche avancée
Re: Exprimer la matrice de A de f dans base canonique
Oui superbe merci j'ai réalisé qu'il était écris que c’était une application linaire et donc qu'on pouvait effectuer des additions et multiplications sur f et donc trouver f(1,0,0) f(0,1,0) et f(0,0,1) en utilisant f(1,1,1) f(1,1,0) et f(0,1,1) J'ai finalement trouvé la matrice et j'ai trouvé comme ...
- 19 Sep 2016, 14:04
- Forum: ✯✎ Supérieur
- Sujet: Exprimer la matrice de A de f dans base canonique
- Réponses: 4
- Vues: 2736
Exprimer la matrice de A de f dans base canonique
Bonjour petite question j'ai un exercice que voici. On considère ere l'application lineaire telle que f \begin{pmatrix} 1\\ 1\\ 0 \end{pmatrix} = \begin{pmatrix} 6\\ 1\\ -3 \end{pmatrix} , f \begin{pmatrix} 0\\ 1\\ 1 \end{pmatrix} = \begin{pmatrix} 4\\ 1\\ -1 \end{pmatrix} ,f \begin{pmatrix} 1\\ 1...
- 19 Sep 2016, 11:21
- Forum: ✯✎ Supérieur
- Sujet: Exprimer la matrice de A de f dans base canonique
- Réponses: 4
- Vues: 2736
Re: Matrice de passage, bloqué sur le système
vecteur de passage : ça ne veut rien dire !!! Oui surement je ne savais pas comment dire" l'un des vecteur de la matrice de passage." Par ailleurs en effet je confond les deux notions si tu peux me dire si c'est bien ça : Donc si on me donne une matrice et qu'on me demande de trouver la m...
- 09 Sep 2016, 16:47
- Forum: ✯✎ Supérieur
- Sujet: Matrice de passage, bloqué sur le système
- Réponses: 23
- Vues: 1283
Re: Matrice de passage, bloqué sur le système
Ah c'est tout ! Il faut juste utiliser le vecteur d'arrivé comme paramètres dans la fonction pour trouver le vecteur de passage ?
merci ^^
merci ^^
- 09 Sep 2016, 14:48
- Forum: ✯✎ Supérieur
- Sujet: Matrice de passage, bloqué sur le système
- Réponses: 23
- Vues: 1283
Re: Matrice de passage, bloqué sur le système
Donc en effet écrire la Matrice A en fonction de 1,0 et 0,1 ce qui revient au système que j'ai écris tout en haut, et que je n'arrive pas a résoudre.
- 09 Sep 2016, 14:32
- Forum: ✯✎ Supérieur
- Sujet: Matrice de passage, bloqué sur le système
- Réponses: 23
- Vues: 1283
Re: Matrice de passage, bloqué sur le système
D'écrire la matrice de la fonction f(x) dans la nouvelle base en occurrence (1,0)(0,1) Check voilà l'exercice que mon prof donne : Ecrire la matrice de f (x; y) = (x + 2y; 4x + 8y) dans la base (1; 0); (0; 1) Ecrire la matrice de f (x; y) = (x + 2y; 4x + 8y) dans la base (1; 1); (1; 2) Ecrire la ...
- 09 Sep 2016, 14:30
- Forum: ✯✎ Supérieur
- Sujet: Matrice de passage, bloqué sur le système
- Réponses: 23
- Vues: 1283
Re: Matrice de passage, bloqué sur le système
Oui je comprend qu'on veut juste la matrice de passage de f mais transformation vers quelque chose... et là c'est 1;0 et 0;1 non ?
Mais si on m'avait dit de l’écrire dans la base , par exemple (1; 1); (1; 2) que faire ?
Désolé hein mais y'a un truc que je pige pas ^^
Mais si on m'avait dit de l’écrire dans la base , par exemple (1; 1); (1; 2) que faire ?
Désolé hein mais y'a un truc que je pige pas ^^
- 09 Sep 2016, 14:21
- Forum: ✯✎ Supérieur
- Sujet: Matrice de passage, bloqué sur le système
- Réponses: 23
- Vues: 1283
Re: Matrice de passage, bloqué sur le système
Ok merci.
Mais on a rien écrit dans la nouvelle base ?
Edit : "En fonction de la nouvelle base"
Mais on a rien écrit dans la nouvelle base ?
Edit : "En fonction de la nouvelle base"
- 09 Sep 2016, 14:14
- Forum: ✯✎ Supérieur
- Sujet: Matrice de passage, bloqué sur le système
- Réponses: 23
- Vues: 1283
Re: Matrice de passage, bloqué sur le système
Donc pour moi la matrice A vaudrait 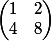
- 09 Sep 2016, 14:10
- Forum: ✯✎ Supérieur
- Sujet: Matrice de passage, bloqué sur le système
- Réponses: 23
- Vues: 1283
Re: Matrice de passage, bloqué sur le système
Ba écoute dans mon cours je n'ai toujours eu que des ensembles de vecteurs a exprimer dans une autre base , jamais un système, si je te demande de l'aide ce n'est pas pour rien enfin... par exemple la base A {a1=(0,1) ;a2=(1,1)} dans une base C {c1=(1,2);c2=(5,4)} Je m'y prend de la façon suivante J...
- 09 Sep 2016, 14:06
- Forum: ✯✎ Supérieur
- Sujet: Matrice de passage, bloqué sur le système
- Réponses: 23
- Vues: 1283
Re: Matrice de passage, bloqué sur le système
Ce que je ME disais
Ceci dit je trouve une matrice certe mais il faut bien l'exprimer en fonction de 1;0 et et 0;1 non ?
Ceci dit je trouve une matrice certe mais il faut bien l'exprimer en fonction de 1;0 et et 0;1 non ?
- 09 Sep 2016, 13:50
- Forum: ✯✎ Supérieur
- Sujet: Matrice de passage, bloqué sur le système
- Réponses: 23
- Vues: 1283
Re: Matrice de passage, bloqué sur le système
Ah okk je me disais qu'il devait devait y avoir quelque chose qui n'allait pas ! Je vais faire ca je reviens ^^
- 09 Sep 2016, 13:43
- Forum: ✯✎ Supérieur
- Sujet: Matrice de passage, bloqué sur le système
- Réponses: 23
- Vues: 1283
Matrice de passage, bloqué sur le système
Bonjour, Petit problème lors d'un changement de base je ne comprend pas je trouve des solutions impossible Ecrire la matrice de f (x; y) = (x + 2y; 4x + 8y) dans la base (1; 0); (0; 1) J'ai donc cherché la matrice de passage mais les systèmes me donnent des valeurs impossibles En exprimant d'abord...
- 09 Sep 2016, 13:32
- Forum: ✯✎ Supérieur
- Sujet: Matrice de passage, bloqué sur le système
- Réponses: 23
- Vues: 1283
Re: Démonstration valeur propres vecteurs prores et SEV
Je vous remercie, je vous cache pas que je comprend pas mais je pense pas qu'on puisse faire plus simple, vous avez l'air d'avoir déjà simplifié au max.
- 07 Sep 2016, 12:21
- Forum: ✯✎ Supérieur
- Sujet: Démonstration valeur propres vecteurs prores et SEV
- Réponses: 9
- Vues: 795
Re: Démonstration valeur propres vecteurs prores et SEV
Ok je te remercie, mais pourquoi Ker() est forcément un SEV ?
- 06 Sep 2016, 13:35
- Forum: ✯✎ Supérieur
- Sujet: Démonstration valeur propres vecteurs prores et SEV
- Réponses: 9
- Vues: 795
Re: Démonstration valeur propres vecteurs prores et SEV
Bon, Une valeur propre c'est selon moi une racine associée au polynôme |A-X*Id|. On va l'appeler ValP Un vecteur propre associée à ValP c'est le noyau de (A-ValP*Id) donc Ker(A-ValP*Id) J'ai lu que Ker(f) = {x appartenant a V | f(x) = 0} et que le noyau est un SEV de L' espace vectoriel V Je suppose...
- 06 Sep 2016, 13:17
- Forum: ✯✎ Supérieur
- Sujet: Démonstration valeur propres vecteurs prores et SEV
- Réponses: 9
- Vues: 795
Démonstration valeur propres vecteurs prores et SEV
Bonjour je voudrai démontrer ceci, mais les démonstrations ne sont pas vraiment mon fort. Démontrer que l’ensemble des vecteurs propres associés à une valeur propre est un sous-espace vectoriel Je sais que pour que F soit un SEV il faut : -F est non vide -F est stable pour l'addition -F est stable p...
- 05 Sep 2016, 18:06
- Forum: ✯✎ Supérieur
- Sujet: Démonstration valeur propres vecteurs prores et SEV
- Réponses: 9
- Vues: 795
Re: Exponentielles de matrices
Merci à vous deux c'est très clair.
- 26 Aoû 2016, 12:46
- Forum: ✯✎ Supérieur
- Sujet: Exponentielles de matrices
- Réponses: 5
- Vues: 2025
Re: Étape d'un calcul
Alors je vais peut être dire une grosse bétise mais
[Rac(n+1)-Rac(n)]x[Rac(n+1)-Rac(n)] = (Rac(n+1)-Rac(n)) au carré
Le carré tue les tue les racines.
Donc tu n'a plus que n+1-n ce qui donne 1 ?
Je suis novice en maths
[Rac(n+1)-Rac(n)]x[Rac(n+1)-Rac(n)] = (Rac(n+1)-Rac(n)) au carré
Le carré tue les tue les racines.
Donc tu n'a plus que n+1-n ce qui donne 1 ?
Je suis novice en maths
- 26 Aoû 2016, 12:36
- Forum: ✎✎ Lycée
- Sujet: Étape d'un calcul
- Réponses: 2
- Vues: 462
Re: Matrice semblable
Merci 
- 24 Aoû 2016, 16:29
- Forum: ✯✎ Supérieur
- Sujet: Matrice semblable
- Réponses: 7
- Vues: 824
- 28 résultats trouvés - Page 1 sur 2 • 1, 2
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
