Forum de Mathématiques: Maths-Forum

Bonjour, j'ai un doute: Quand on a une tâche d'Airy (une figure de diffraction) est-ce la même chose qu'une figure d'interférence ? Autrement dit, est-ce que c'est la diffraction en elle même qui provoque la tâche d'Airy (ou toute autre figure de diffraction) ou c'est l'interférence résultante de la...

J'ai plusieurs questions concernant les intégrales : Les intégrales multiples, je crois bien que ça s'associe à des fonctions à plusieurs variables. Or si j'ai bien compris le principe, il s'agit simplement de transformer une intégrale multiple en plusieurs (une somme peut être ???) intégrale simple...

Je vois, et pour cette question : Soit \varphi , la fonction définie par \forall x \in \mathbb{R} \varphi(x) = f(x) \oplus g(x) \otimes h(x), \varphi : \mathbb{R}\rightarrow\mathbb{R} où \oplus et \otimes sont deux opérations identiques ou réciproques (je sais pas si ...

Merci paquito. Et pour la situation inverse ? Soit \Phi une fonction qu'on définies ainsi : \forall x, y, z \in \R, \Phi : x, y, z \to \Phi(x, y, z) . On définies ses dérivées partielles par éventuellement des conditions : \frac{\partial \Phi}{\partial x}, \frac{\partial \Phi}{\partial y}, \...

Et si on exprime \gamma en fonction de \alpha et \beta , on peut lui associer deux dérivée partielles, que signifie la dérivée simple de la fonction à une variable ? Je vois pas en fait le sens de cette dérivée... Exemple : Soit \phi une fonction à plusieurs variables définie par \forall x, y \in \m...

Soit fonction d'une variable définie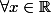
Maintenant, soit le '' changement de variables suivants '' où * est une des 4 opérations usuelles.
Que représente la quantité par rapport à et ?

Cette fonction, discontinue en 0, ne sera jamais dérivable en 0! Où est le problème? Pour l'intégrale, si on modifie la valeur de f en un nombre fini de points, cela ne change rien, donc, \bigint_{0}^{+oo}f(t)dt=0 . Je vois, je me complique la vie pour rien ^^, c'est souvent le cas quand on...

Je vois, l'expression algébrique n'est pas une finen soi (c'est suffisant mais pas nécessaire !!!) mais pour calculer une dérivée ou une primitive de cette fonction, il faut bien avoir son expression algébrique ?

Le fait de définir la fonction en deux morceaux ne convient pas ? Par exemple : f(x) = 1 si x 0, ça ne va pas ? En une seule formule, on pourrait avoir : f(x) = E\left\( 1 - \frac{2}{\pi}\arctan(x) \right\) où E désigne la partie entière. Si, ça me convient ! Merci pour la f...

Ça serait une sorte du fonction de Heaviside à une valeur près : 0...

Peut on dire que par les propriétés sur R+, la fonction est affine par morceau sur R+ ?
Sinon, je cherche en fait à déterminer l'expression algebrique d'au moins une fonction vérifiant les conditions (même s'il y en a une infinité...)

Bonjour, je cherche pour des contraintes de calcul, une fonction tel que sur

et

Je ne vois pas du tout comment m'y prendre sachant que sur la fonction peut à priori se comporter de manière arbitraire...

C'était pour savoir si c'était possible de calculer une somme (avec le signe sigma) de n termes avec n \in \mathbb{R} (ou n \in \mathbb{C}) ou plus généralement: n \in E où \mathbb{N} \subset E ? Apparemment c'est possible puisqu'un programme adapté peut attribuer une valeur à ce type d'obje...

Je ne sais absolument pas si on peut sommer un nombre non entier de termes, et je ne sais absolument pas comment faire, j'ai testé quelques identités à l'ordi où une somme de pi termes est réalisée et bien définie, à l'ordi on a: \bigsum_{k=0}^{\pi} \frac{k}{\pi}^2 + \frac{1}{\pi} = 1 \bigsum_{k=0}^...

Bonjour, n'étant pas du tout un pro dans les résolutions d'EDP, je me demandais si il existait une solution unique à ce système d'EDP : \frac{\partial}{\partial x} f(x, y, z) = 0 ET \frac{\partial}{\partial y} f(x, y, z) + \frac{\partial}{\partial z} f(x, y, z) = 0 Merci d'av...