le voila , Merci d'avance
967 résultats trouvés
Revenir à la recherche avancée
- 10 Aoû 2016, 21:32
- Forum: ✯✎ Supérieur
- Sujet: equation complexe
- Réponses: 5
- Vues: 438
Re: equation complexe
si, regardez la dernière partie du photo
- 10 Aoû 2016, 21:16
- Forum: ✯✎ Supérieur
- Sujet: equation complexe
- Réponses: 5
- Vues: 438
equation complexe
Bonjour,
résoudre l'équation suivante:
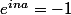
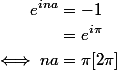
mais pourquoi ils ont écrit :
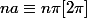
Merci d'avance
résoudre l'équation suivante:
mais pourquoi ils ont écrit :
Merci d'avance
- 10 Aoû 2016, 21:03
- Forum: ✯✎ Supérieur
- Sujet: equation complexe
- Réponses: 5
- Vues: 438
Re: suite
Bonsoir,
quand est ce que cette série est convergente
Merci d'avance
quand est ce que cette série est convergente
Merci d'avance
- 29 Juil 2016, 19:44
- Forum: ✯✎ Supérieur
- Sujet: suite
- Réponses: 3
- Vues: 390
suite
Bonjour,
y-a-t-il quelqu'un qui peut détailler ces calcules Merci d'avance
^{n}\sqrt{2\pi n})
y-a-t-il quelqu'un qui peut détailler ces calcules Merci d'avance
- 29 Juil 2016, 14:42
- Forum: ✯✎ Supérieur
- Sujet: suite
- Réponses: 3
- Vues: 390
Re: DL serie harmonique
Bonjour,
Merci beaucoup
Merci beaucoup
- 26 Juil 2016, 17:49
- Forum: ✯✎ Supérieur
- Sujet: DL serie harmonique
- Réponses: 4
- Vues: 429
Re: DL serie harmonique
Bonjour,
pour l'expression à gauche :
Pourquoi ils ont utilisé cette remarque au lieu d'utiliser le théorème directement ?
pour l'expression à gauche :
Pourquoi ils ont utilisé cette remarque au lieu d'utiliser le théorème directement ?
- 26 Juil 2016, 12:58
- Forum: ✯✎ Supérieur
- Sujet: DL serie harmonique
- Réponses: 4
- Vues: 429
DL serie harmonique
Bonjour, voila proposition de comparaison d'une serie à une integrale: 0.jpg ici il ont pris la serie harmonique comme applcation mais je ne comprend pas le choix des bornes qu'ils ont choisissent quelqu'un peux m'expliquer ca ? 1.jpg Pour moi, on doit avoir: n \geq 2\ 1=n_0=p,\ q=n \displaystyle \i...
- 26 Juil 2016, 11:42
- Forum: ✯✎ Supérieur
- Sujet: DL serie harmonique
- Réponses: 4
- Vues: 429
Re: nature de serie
donc l'explication pour le 4 eme vient de
si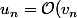) et
et 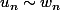 alors
alors 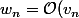)
n'est ce pas sinon tu peux m'explique d'ou vient le 4eme
Merci d'avance
si
n'est ce pas sinon tu peux m'explique d'ou vient le 4eme
Merci d'avance
- 26 Juil 2016, 08:19
- Forum: ✯✎ Supérieur
- Sujet: nature de serie
- Réponses: 8
- Vues: 572
Re: nature de serie
Bonjour
je veux dire la 3eme propriété
je veux dire la 3eme propriété
- 25 Juil 2016, 19:05
- Forum: ✯✎ Supérieur
- Sujet: nature de serie
- Réponses: 8
- Vues: 572
Re: nature de serie
Bonjour,
merci c'est très gentil de ta part mais je suis intéressé par 4eme question je pense qu'il sont basé sur le fait que
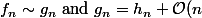$ then $f_n=h_n+\mathcal{O}(n))
Merci d'avance
merci c'est très gentil de ta part mais je suis intéressé par 4eme question je pense qu'il sont basé sur le fait que
Merci d'avance
- 25 Juil 2016, 16:34
- Forum: ✯✎ Supérieur
- Sujet: nature de serie
- Réponses: 8
- Vues: 572
nature de serie
Bonjour, Soit \sum_{n\geq 0}(-1)^{n}u_n avec \begin{cases} u_0\in\mathbb{R}^{+}\\\forall n\in\mathbb{N},\quad u_{n+1}=\dfrac{e^{-u_n}}{n+1}\\ \end{cases} je n'ai pas compris à quoi ca sert de dire ca : u_{n+1}\sim\dfrac{1}{n+1} \implies u_n\sim\dfrac{1}{n} de plus je n'arrive pas a comprendr...
- 25 Juil 2016, 13:36
- Forum: ✯✎ Supérieur
- Sujet: nature de serie
- Réponses: 8
- Vues: 572
Re: Q-asympotote
Oui surtout pour l’utiliser dans la détermination de la nature des séries
- 16 Juil 2016, 17:14
- Forum: ✯✎ Supérieur
- Sujet: Q-asympotote
- Réponses: 7
- Vues: 444
Re: Q-asympotote
Bonjour,
Est ce que vous connaissez des livres qui traitent ce genre d'exercices Merci d'avance
Est ce que vous connaissez des livres qui traitent ce genre d'exercices Merci d'avance
- 16 Juil 2016, 08:35
- Forum: ✯✎ Supérieur
- Sujet: Q-asympotote
- Réponses: 7
- Vues: 444
Re: Q-asympotote
Bonsoir,
@ samoufar donc comme il a dit @Razes doit être figurer dans l’égalité puis voir la plus précis parmi eux
Merci beaucoup
@ samoufar donc comme il a dit @Razes doit être figurer dans l’égalité puis voir la plus précis parmi eux
Merci beaucoup
- 15 Juil 2016, 23:52
- Forum: ✯✎ Supérieur
- Sujet: Q-asympotote
- Réponses: 7
- Vues: 444
Q-asympotote
Bonsoir, \begin{aligned}e^{-\tan\left(\frac{\pi}{4}+\frac1n\right)\log(n)}&=\left(\dfrac1n-2\dfrac{\log(n)}{n^2}-2\dfrac{\log(n)}{n^3}+O\left(\frac{\log^2(n)}{n^3}\right)\right)\\&=\frac1n +O\left(\frac{\log(n)}{n^2}\right&#...
- 15 Juil 2016, 22:29
- Forum: ✯✎ Supérieur
- Sujet: Q-asympotote
- Réponses: 7
- Vues: 444
Re: asymptote ( terme cosn )
Bonsoir,
Merci
Merci
- 15 Juil 2016, 22:08
- Forum: ✯✎ Supérieur
- Sujet: asymptote ( terme cosn )
- Réponses: 2
- Vues: 327
asymptote ( terme cosn )
Bonjour,

votre aide svp comment je peux se débarrasser de)

votre aide svp comment je peux se débarrasser de
- 15 Juil 2016, 13:14
- Forum: ✯✎ Supérieur
- Sujet: asymptote ( terme cosn )
- Réponses: 2
- Vues: 327
Re: asymptote
Bonjour,
oui comme il a dit : @ samoufar
oui comme il a dit : @ samoufar
- 15 Juil 2016, 09:28
- Forum: ✯✎ Supérieur
- Sujet: asymptote
- Réponses: 7
- Vues: 362
Re: asymptote
Bonjour, oui j'ai trompé voila : puisque : \mathcal{O}\left(\dfrac{1}{n^{3}} \right)+\mathcal{O}\left( \dfrac{\ln(n)}{n^{4}}\right)=\mathcal{O}\left(\dfrac{\ln(n)}{n^{2}} \right) en effet , \frac{\dfrac{1}{n^3}}{\dfrac{\ln(n)}{n^2}} \xrightarrow[n\to\i...
- 14 Juil 2016, 21:08
- Forum: ✯✎ Supérieur
- Sujet: asymptote
- Réponses: 7
- Vues: 362
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
