y-a-t-il quelqu'un qui peut détailler ces calcules Merci d'avance
- Untitled.jpg (11.03 Kio) Vu 429 fois
Suite
4 messages
- Page 1 sur 1
Re: suite
par samoufar » 30 Juil 2016, 16:22
Bonjour,
Est-ce que tu disposes de la formule de Stirling ? Sinon la démonstration classique se fait à l'aide des intégrales de Wallis (un petit tour sur un moteur de recherche s'impose si tu veux en savoir plus
).
En tout cas essaies de transformer tes factorielles à l'aide de cette formule, en gardant en tête qu'il est possible de multiplier des équivalents (en l'occurence ic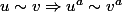i
si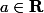 
).
Il suffit de l'écrire, ça marche tout seul
Est-ce que tu disposes de la formule de Stirling ? Sinon la démonstration classique se fait à l'aide des intégrales de Wallis (un petit tour sur un moteur de recherche s'impose si tu veux en savoir plus
).En tout cas essaies de transformer tes factorielles à l'aide de cette formule, en gardant en tête qu'il est possible de multiplier des équivalents (en l'occurence ici
Il suffit de l'écrire, ça marche tout seul
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :