Bonsoir,
Je ne comprends pas bien quelle relation lie le développement limité de f a son développement en série entière. A l'instar du DL, toute fonction f est-elle développable en série entière, sous réserve qu'on soit dans le rayon de convergence associé? Comment passe-t-on de l'un à l'autre? Merci de vos lumières.
Développement en séries entière versus DL
2 messages
- Page 1 sur 1
Salut,
Si tu pose la question "théorique", c'est à dire dans le cas le plus général possible, on a :
1) SI une fonction f est développable en série entière au voisinage de avec un rayon de convergence
avec un rayon de convergence 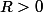 ALORS elle admet au voisinage de
ALORS elle admet au voisinage de  des développements limités de tout ordre et on obtient ces D.L. tout simplement en "tronquant" la série.
des développements limités de tout ordre et on obtient ces D.L. tout simplement en "tronquant" la série.
2) Il existe des fonction de classe (indéfiniement dérivables) sur R, donc admettant des D.L. de tout ordre en tout point
(indéfiniement dérivables) sur R, donc admettant des D.L. de tout ordre en tout point  de R MAIS non développable en série entière au voisiange de certains
de R MAIS non développable en série entière au voisiange de certains  . Par exemple la fonction
. Par exemple la fonction =\exp(-\frac{1}{x^2})) pour
pour 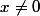 et
et =0) est
est  au voisinage de 0 (pourquoi ?) mais n'est pas développable en série entière au voisinage de 0 (pourquoi ?)
au voisinage de 0 (pourquoi ?) mais n'est pas développable en série entière au voisinage de 0 (pourquoi ?)
Si tu pose la question "théorique", c'est à dire dans le cas le plus général possible, on a :
1) SI une fonction f est développable en série entière au voisinage de
2) Il existe des fonction de classe
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
