Primitive de a^x
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Fouxti
- Messages: 4
- Enregistré le: 30 Nov 2013, 11:02
-
par Fouxti » 30 Nov 2013, 11:33
Bonjour,
la primitive de a^x semble pouvoir se trouver immédiatement, je voulais savoir doù ça venait mais je n'arrive pas à dériver la primitive pour retomber sur a^x, primitive qui dans mon cours est : a^x/ln a
')
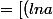(a^x)(ln a) - ((a^x)/a) ] / (ln a)^2)
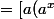(lna)^2 - (a^x)] / a(lna)^2)
On peut mettre les a^x en évidence mais après je coince.
Merci d'avance,
Foux.
-
Fred_Sabonnères
- Membre Relatif
- Messages: 221
- Enregistré le: 07 Oct 2007, 16:04
-
par Fred_Sabonnères » 30 Nov 2013, 11:39
Tu pars du fait que
Une primitive de
est
Tu appliques bêtement en remplaçant k par Lna
-
Fred_Sabonnères
- Membre Relatif
- Messages: 221
- Enregistré le: 07 Oct 2007, 16:04
-
par Fred_Sabonnères » 30 Nov 2013, 11:44
Pardon. J'ai mal lu ta question
La dérivée de
est
'= (e^{x Ln a})'=Lna \times e^{x Ln a}=Lna \times a^x)
-
Fouxti
- Messages: 4
- Enregistré le: 30 Nov 2013, 11:02
-
par Fouxti » 30 Nov 2013, 12:08
Par contre j'ai un soucis avec x = e^lnx
-
Fred_Sabonnères
- Membre Relatif
- Messages: 221
- Enregistré le: 07 Oct 2007, 16:04
-
par Fred_Sabonnères » 30 Nov 2013, 12:11
car la fonction exponentielle est la bijection réciproque de la fonction logarithme népérien
d'où
or
d'où le résultat
-
Fouxti
- Messages: 4
- Enregistré le: 30 Nov 2013, 11:02
-
par Fouxti » 30 Nov 2013, 12:27
Sa Majesté a écrit:Tu sembles appliquer la formule de dérivée d'un quotient
' = \frac{u'v-uv'}{v^2})
Mais ce n'est pas ce qu'il faut faire puisque a est une constante, ln(a) aussi
C'est vrai que c'est tout de suite plus facile de dériver 1/lna(a^x)' :mur:
Merci !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
