Equation trigonométrique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
tchetchene
- Membre Naturel
- Messages: 22
- Enregistré le: 21 Aoû 2013, 12:41
-
 par tchetchene » 04 Nov 2013, 18:23
par tchetchene » 04 Nov 2013, 18:23
Bonjour,
je fais un exercice de cours et je n'arrive pas.
transformez :
E = (cosx - sinx) / (cosx + sinx)
merci de votre aide

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 04 Nov 2013, 19:09
par chan79 » 04 Nov 2013, 19:09
tchetchene a écrit:Bonjour,
je fais un exercice de cours et je n'arrive pas.
transformez :
E = (cosx - sinx) / (cosx + sinx)
merci de votre aide
salut
sin x=cos(pi/2 - x)
tu dois arriver à
)
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 04 Nov 2013, 19:39
par Carpate » 04 Nov 2013, 19:39
chan79 a écrit:salut
sin x=cos(pi/2 - x)
Variante :
}{cos(x-\frac{\pi}{4})})

-
Sa Majesté
- Membre Transcendant
- Messages: 6275
- Enregistré le: 23 Nov 2007, 14:00
-
 par Sa Majesté » 04 Nov 2013, 20:44
par Sa Majesté » 04 Nov 2013, 20:44
tchetchene a écrit:transformez :
E = (cosx - sinx) / (cosx + sinx)
merci de votre aide
Transformer, c'est un peu vague. Tu n'as pas d'autres informations ?
-
tchetchene
- Membre Naturel
- Messages: 22
- Enregistré le: 21 Aoû 2013, 12:41
-
 par tchetchene » 04 Nov 2013, 22:27
par tchetchene » 04 Nov 2013, 22:27
Sa Majesté a écrit:Transformer, c'est un peu vague. Tu n'as pas d'autres informations ?
il me demande de metre sous la forme d'un produit de facteurs les expressions:
cosx - sinx
et cosx + sinx
et ensuite d'en déduire une tranformation de la fraction
E = (cosx-sinx)/(cosx+sinx)
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 05 Nov 2013, 11:23
par Carpate » 05 Nov 2013, 11:23
Carpate a écrit:Variante :
}{cos(x-\frac{\pi}{4})})
}{cos(x-\frac{\pi}{4})}=\frac{cos(\frac{\pi}{2}+(x-\frac{\pi}{4}))}{cos(x-\frac{\pi}{4})}=\frac{-sin(x-\frac{\pi}{4})}{cos(x-\frac{\pi}{4})}=-tg(x-\frac{\pi}{4})=+tg(\frac{\pi}{4}-x))
-
tchetchene
- Membre Naturel
- Messages: 22
- Enregistré le: 21 Aoû 2013, 12:41
-
 par tchetchene » 05 Nov 2013, 22:54
par tchetchene » 05 Nov 2013, 22:54
Carpate a écrit:}{cos(x-\frac{\pi}{4})}=\frac{cos(\frac{\pi}{2}+(x-\frac{\pi}{4}))}{cos(x-\frac{\pi}{4})}=\frac{-sin(x-\frac{\pi}{4})}{cos(x-\frac{\pi}{4})}=-tg(x-\frac{\pi}{4})=+tg(\frac{\pi}{4}-x))
Comment tu peux mettre rc2/2 partout?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 06 Nov 2013, 07:55
par Carpate » 06 Nov 2013, 07:55
tchetchene a écrit:Comment tu peux mettre rc2/2 partout?
Comment ? parce que
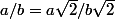
La vraie question c'est pourquoi ? Pour introduire cos(pi/4) et sin(pi/4)
Ton titre annonce une équation mais je n'en vois pas ...
-
tchetchene
- Membre Naturel
- Messages: 22
- Enregistré le: 21 Aoû 2013, 12:41
-
 par tchetchene » 06 Nov 2013, 08:36
par tchetchene » 06 Nov 2013, 08:36
Carpate a écrit:Comment ? parce que
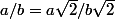
La vraie question c'est pourquoi ? Pour introduire cos(pi/4) et sin(pi/4)
Ton titre annonce une équation mais je n'en vois pas ...
oui je me suis trompé pour le titre de l'annonce.
le produit de facteur de (cosx - sinx) serait donc RC2/2(cosx - sinx)?
-
tchetchene
- Membre Naturel
- Messages: 22
- Enregistré le: 21 Aoû 2013, 12:41
-
 par tchetchene » 06 Nov 2013, 10:26
par tchetchene » 06 Nov 2013, 10:26
chan79 a écrit:salut
sin x=cos(pi/2 - x)
tu dois arriver à
)
en faisant cela, j'arrive à :
( 2cosx - cos(PI/2)) / cos (PI/2)
mais je ne vois pas tan (pi/4)

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 06 Nov 2013, 10:41
par chan79 » 06 Nov 2013, 10:41
salut
On peut faire comme suit, mais ce n'est pas mieux que les autres méthodes proposées.
-cos(\fra{\pi}{2}-x)}{cos(x)+cos(\fra{\pi}{2}-x)})
ensuite tu utlises les formules cos p+cos q= .. et cos p-cosq=...
sin(x-\fra{\pi}{4})}{2cos(\fra{\pi}{4})cos(x-\fra{\pi}{4})})
sin(pi/4)=cos(pi/4)
on obtient
=tan(\fra{\pi}{4}-x))
-
tchetchene
- Membre Naturel
- Messages: 22
- Enregistré le: 21 Aoû 2013, 12:41
-
 par tchetchene » 06 Nov 2013, 10:51
par tchetchene » 06 Nov 2013, 10:51
chan79 a écrit:salut
On peut faire comme suit, mais ce n'est pas mieux que les autres méthodes proposées.
-cos(\fra{\pi}{2}-x)}{cos(x)+cos(\fra{\pi}{2}-x)})
ensuite tu utlises les formules cos p+cos q= .. et cos p-cosq=...
sin(x-\fra{\pi}{4})}{2cos(\fra{\pi}{4})cos(x-\fra{\pi}{4})})
sin(pi/4)=cos(pi/4)
on obtient
=tan(\fra{\pi}{4}-x))
merci beaucoup, j'ai compris
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
