Calcul de limites.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Biologue
- Messages: 2
- Enregistré le: 11 Juil 2012, 22:49
-
 par Biologue » 04 Nov 2013, 17:20
par Biologue » 04 Nov 2013, 17:20
Bonjour,
Je n'ai pas fait de mathématiques depuis plus d'un an, et je
dois m'y remettre Cependant, je suis
vraiment rouillé...
Pouvez-vous me guider pour calculer ces limites?
1)
=\frac {sqrt{1+x} - sqrt{1-x}} {x}<br /><br />= \lim_{x \to 0} \frac {(sqrt{1+x} - sqrt{1-x}) . (sqrt{1+x}+sqrt{1-x})} {x.(sqrt{1+x}+sqrt{1-x})}<br /><br /><br />= \lim_{x \to 0} \frac {2x} { x.(sqrt{1+x}+sqrt{1-x})}<br /><br />Finalement: \lim_{x \to 0} f(x)= 1)
2)
= sqrt{x+sqrt{x+sqrt{x}}}-sqrt{x}<br /><br />= \lim_{x \to +\infty} (sqrt{x+sqrt{x+sqrt{x}}}-sqrt{x}) . (sqrt{x+sqrt{x+sqrt{x}}}+sqrt{x})<br />= \lim_{x \to +\infty} sqrt{x+sqrt{x}}<br />= \lim_{x \to +\infty} sqrt{(sqrt{x}+1).sqrt{x}} <br />= + \infty)
1) et 2) sont-ils correctes?
3)

et je bloque sur celle-ci . // ne faudrait-il pas utiliser
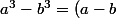 (a^2+ab+b^2))
soit
= \frac {a^3-b^3} {a^2+ab+b^2})
avec

et

Je vous remercie.
edit: comment mettre à la ligne et espacer en LATEX?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 04 Nov 2013, 17:59
par Carpate » 04 Nov 2013, 17:59
Biologue a écrit:Bonjour,
Je n'ai pas fait de mathématiques depuis plus d'un an, et je
dois m'y remettre Cependant, je suis
vraiment rouillé...
Pouvez-vous me guider pour calculer ces limites?
1)
=\frac {sqrt{1+x} - sqrt{1-x}} {x}<br /><br />= \lim_{x \to 0} \frac {(sqrt{1+x} - sqrt{1-x}) . (sqrt{1+x}+sqrt{1-x})} {x.(sqrt{1+x}+sqrt{1-x})}<br /><br /><br />= \lim_{x \to 0} \frac {2x} { x.(sqrt{1+x}+sqrt{1-x})}<br /><br />Finalement: \lim_{x \to 0} f(x)= 1)
2)
= sqrt{x+sqrt{x+sqrt{x}}}-sqrt{x}<br /><br />= \lim_{x \to +\infty} (sqrt{x+sqrt{x+sqrt{x}}}-sqrt{x}) . (sqrt{x+sqrt{x+sqrt{x}}}+sqrt{x})<br />= \lim_{x \to +\infty} sqrt{x+sqrt{x}}<br />= \lim_{x \to +\infty} sqrt{(sqrt{x}+1).sqrt{x}} <br />= + \infty)
1) et 2) sont-ils correctes?
3)

et je bloque sur celle-ci . // ne faudrait-il pas utiliser
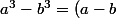 (a^2+ab+b^2))
= \frac {a^3-b^3} {a^2+ab+b^2} avec a= sqrt[3] {x+1} et b= sqrt[3] {x})
Je vous remercie.
edit: comment mettre à la ligne en LATEX?
1) est correct
2) il manque le dénominateur
3) utilise la multiplication par la quantité conjuguée pour lever l'indétermination, on obtient :
^2}}{1+\sqrt[3]{\frac{x}{x+1}})
qui tend vers 0
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 05 Nov 2013, 14:25
par Carpate » 05 Nov 2013, 14:25
Carpate a écrit:1) est correct
2) il manque le dénominateur
3) utilise la multiplication par la quantité conjuguée pour lever l'indétermination, on obtient :
^2}}{1+\sqrt[3]{\frac{x}{x+1}})
qui tend vers 0
=sqrt{x+\sqrt{x+\sqrt{x}}}-\sqrt{x}=\frac{\sqrt{x+\sqrt{x}}}{\sqrt{x+\sqrt{x+sqrt{x}}}+\sqrt{x}})
En divisant haut et bas par

:
=\frac{\sqrt{1+\frac{\sqrt{x}}{x}}}{ \sqrt{1+\sqrt{\frac{x+\sqrt{x}}{x^2}}+1})
qui tend vers
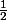
en

-
Biologue
- Messages: 2
- Enregistré le: 11 Juil 2012, 22:49
-
 par Biologue » 05 Nov 2013, 19:43
par Biologue » 05 Nov 2013, 19:43
Carpate a écrit:=sqrt{x+\sqrt{x+\sqrt{x}}}-\sqrt{x}=\frac{\sqrt{x+\sqrt{x}}}{\sqrt{x+\sqrt{x+sqrt{x}}}+\sqrt{x}})
En divisant haut et bas par

:
=\frac{\sqrt{1+\frac{\sqrt{x}}{x}}}{ \sqrt{1+\sqrt{\frac{x+\sqrt{x}}{x^2}}+1})
qui tend vers
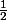
en

Bonsoir,
Tout d'abord, je vous remercie. Vous m'avez été d'une aide précieuse

Concernant ceci:
=\frac{\sqrt{1+\frac{\sqrt{x}}{x}}}{ \sqrt{1+\sqrt{\frac{x+\sqrt{x}}{x^2}}+1})
je ne vois pas d'où viens le

,
ayant fais le calcul, je me retrouve avec
=\frac{\sqrt{1+\frac{\sqrt{x}}{x}}}{ \sqrt{1+\sqrt{\frac{x+\sqrt{x}}{x}}+1})
=>

non?
Pouvez-vous m'expliquer s.v.p ?
Cordialement,

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 05 Nov 2013, 22:18
par chan79 » 05 Nov 2013, 22:18
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 201 invités
