Triangle isocele

[jean94500]

bonjour j'aurai besoin d'aide pour cette exercice

1)on considère la propriété suivante : si un triangle est isocéle,alors il a deux angles égaux

a)écrire l'énoncé réciproque de cette propriété

b)cet énoncé réciproque est-il vrai ?s i oui écrire l'énoncé et l'énoncé réciproque en une seule phrase

merci pour votre aide

[busard_des_roseaux]

bonjour,

la définition d'un triangle ABC isocèle de sommet A est la suivante:


il admet un axe de symétrie passant par A, ie, par pliage, on peut superposer
les deux triangles symétriques.

un triangle ABC isocèle en A a deux côtés égaux AB et AC et deux angles égaux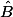 et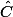

Pour la réciproque, on prend la conclusion comme hypothèse et l'hypothèse comme conclusion

"si alors " et "si alors " sont réciproques l'une de l'autre.

La réciproque s'énonce:
si un triangle ABC a deux angles égaux de sommet B et C, alors il est isocèle en A.


démo
j'espère que tu sais ce qu'est un sinus d'un angle. Il se trouve que dans tout triangle
non aplati , les longueurs des côtés et les sinus des angles forment un
tableau de proportionnalité


AB AC BC
sin(C) sin(B) sin(A)

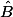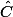donc , si les angles et sont égaux, alors les côtés [AB] et [AC] ont même longueur.

maintenant, si tu considères la médiane (AH), les triangles AHB et AHC ont les mêmes
dimensions , ce qui fait que (AH) est
médiatrice de [BC] donc axe de symétrie de ABC.

La réciproque est donc vraie.

[jean94500]

Pour la question A j'ai compris ta réponse mais pour la B je n'aie pas compris

[busard_des_roseaux]

en fait, la réciproque est vraie.

si les deux angles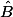 et 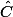sont égaux, si (AH) est médiane de ABC issue de A, alors elle est médiatrice de [BC] et donc ABC est isocèle en A.


pour (b), c'est plus compliqué.

quand on écrit "si A alors B" , B est une condition nécessaire pour A
on pense "A est vraie seulement si B est vraie"

La réciproque est
"si B alors A"
on pense "A est vraie si B est vraie"

quand la proposition "si A alors B" et la proposition "si B alors A" sont vraies,
on écrit A si, et seulement si, B (sous entendu : sont vraies)

[jean94500]

Et je doit mettre quoi comme réponses ?

[busard_des_roseaux]

1)on considère la propriété suivante : si un triangle est isocéle,alors il a deux angles égaux


]si un triangle a deux angles égaux, alors il est isocèle

b)cet énoncé réciproque est-il vrai ?s i oui écrire l'énoncé et l'énoncé réciproque en une seule phrase
oui

un triangle est isocèle à condition qu'il ait deux angles égaux et uniquement dans ce cas