Voila un exercice que j'ai vu il y'a très longtemps mais je ne me souviens plus de la méthode à faire.
Je dois trouvez l'équation des tangentes ou demi-tangentes en x=1;x=3;x=0 pour f(x) = |x-1| ;) (9-x²)
le truc c'est que je ne sais meme plus ce que qu'il faut faire et ca m'arrangerais d'avoir les détails des étaps si possible
Si quelqu'un pouvait m'aider ca serait bien gentil :)
Tangente
8 messages
- Page 1 sur 1
sorahh a écrit:Voila un exercice que j'ai vu il y'a très longtemps mais je ne me souviens plus de la méthode à faire.
Je dois trouvez l'équation des tangentes ou demi-tangentes en x=1;x=3;x=0 pour f(x) = |x-1|(9-x²)
le truc c'est que je ne sais meme plus ce que qu'il faut faire et ca m'arrangerais d'avoir les détails des étaps si possible
Si quelqu'un pouvait m'aider ca serait bien gentil
Salut !
Si
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
capitaine nuggets a écrit:Salut !
Siest dérivable en
alors une équation de la tangente
à
en
est :
heu.. je dois remplacer x par A dans la fonction de départ, PUIS, calculer la dérivé et remplacer le x de la dérivé par a et voir si le nombre de la dérivé = le nombre de la fonction ou bien je me gourre?
Désolé mais je ne trouve pas claire l'explication :/
Kiocle a écrit:Quand tu regarde x-1 si x = 1.00001 x-1>0 on dit que x est 1+
pour 1- x = 0.0009 et x - 1 < 0
Donc quand tu passe à la valeur absolue ça change.
De même pour 3+ si x = 3.00001et la racine n'est pas bien définie.
Alors que pour 3-, x=2.99999 il n'y a pas de problème.
Pour dériver pense que
ha oui! je me souviens mtn pour les valeurs absolue ^^
Mais après que j'ai dérivé la fonction. Qu'est ce que je dois faire du coup?
La fonction dérivé donne :

Tu cherche la tangente en 1, tu evalue donc f'(a) pour appliquer la formule.
mais
 si x=1+
si x=1+
 si x = 1-
si x = 1-
d'ou = \sqrt{8})
 = -\sqrt{8})
En 1+ il s'agit de la demi tangente à droite en 1- de la demi tangente à gauche.
Tu utilise la formule avec a=1- a=1+ puis pour 3 (avec éventuellement 3+ et 3- si besoin).
Pour 1+ tu obtient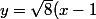)
Tu cherche la tangente en 1, tu evalue donc f'(a) pour appliquer la formule.
mais
d'ou
En 1+ il s'agit de la demi tangente à droite en 1- de la demi tangente à gauche.
Tu utilise la formule avec a=1- a=1+ puis pour 3 (avec éventuellement 3+ et 3- si besoin).
Pour 1+ tu obtient
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
