Bonjour tout le monde,
Voila j'ai réalisé la décomposition en série de Fourier d'un signal trapèze. Ça m'a pris pas mal de temps, je suis arrivé à la quasi toute fin de ma démonstration et j'ai un cosinus qui me pose problème :ptdr:
Je trouve les coefficients an=0 et les bn paires aussi. J'ai donc :
b_n = 12/((n*PI)²)*2*sin(nPI/2)*cos(nPI/3)
Je pose donc n = 2p+1
et sin(nPI/2) devient égal à (-1)^p
j'ai donc :
b_2p+1 = 12/(((2p+1)*PI)²)*2*(-1)^p*cos((2p+1)*PI/3)
Et je suis bloqué ici :hum: j'aimerai me débarrasser du cosinus, un peu comme j'ai fais avec le sinus mais impossible de trouver la méthode.
Je remarque que c'est aussi circulaire, en passant de -1 ; 1/2 ; 1/2 et ainsi de suite.
Voila en espérant mettre fais compris et avoir de l'aide.
Merci d'avance.
Simplification série de Fourier
5 messages
- Page 1 sur 1
bartras a écrit:Bonjour tout le monde,
Voila j'ai réalisé la décomposition en série de Fourier d'un signal trapèze. Ça m'a pris pas mal de temps, je suis arrivé à la quasi toute fin de ma démonstration et j'ai un cosinus qui me pose problème :ptdr:
Je trouve les coefficients an=0 et les bn paires aussi. J'ai donc :
b_n = 12/((n*PI)²)*2*sin(nPI/2)*cos(nPI/3)
Je pose donc n = 2p+1
et sin(nPI/2) devient égal à (-1)^p
j'ai donc :
b_2p+1 = 12/(((2p+1)*PI)²)*2*(-1)^p*cos((2p+1)*PI/3)
Et je suis bloqué ici :hum: j'aimerai me débarrasser du cosinus, un peu comme j'ai fais avec le sinus mais impossible de trouver la méthode.
Je remarque que c'est aussi circulaire, en passant de -1 ; 1/2 ; 1/2 et ainsi de suite.
Voila en espérant mettre fais compris et avoir de l'aide.
Merci d'avance.
Pourrais-tu donner un peu plus de précisions sur ton "signal trapèze" ?
Pythales a écrit:Pourrais-tu donner un peu plus de précisions sur ton "signal trapèze" ?
Bonsoir,
Bien sur, alors il s'agit d'un trapèze de période 2*PI, d'amplitude -1 à 1.
[0;PI/6] : f(tétha) = PI/6 * théta
[PI/6;5PI/6] : f(tétha) = 1
[5PI/6;PI] : f(tétha) = 6 ( 1 - théta/PI )
Voila, et c'est symétrique en -1 par rapport à l'axe des ordonnées.
bartras a écrit:Bonsoir,
Bien sur, alors il s'agit d'un trapèze de période 2*PI, d'amplitude -1 à 1.
[0;PI/6] : f(tétha) = PI/6 * théta
[PI/6;5PI/6] : f(tétha) = 1
[5PI/6;PI] : f(tétha) = 6 ( 1 - théta/PI )
Voila, et c'est symétrique en -1 par rapport à l'axe des ordonnées.
Je vois ton problème, mais je ne crois pas qu'on puisse trouver une formule générale pour
A titre de comparaison, si au lieu de
et là encore il n'est pas possible de donner une formule générale.
Bonjour
En utilisant la relation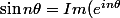=Im((e^{i\theta})^n)) et les sommes de séries entières
et les sommes de séries entières  (où on posera ensuite
(où on posera ensuite  (séries entières à lacunes ?) (séries à trouver) on pourra peut-être s'en tirer.
(séries entières à lacunes ?) (séries à trouver) on pourra peut-être s'en tirer.
Remarques.
On n'aura pas de problèmes de convergences pour puisque les
puisque les  vont vérifier quelque chose type
vont vérifier quelque chose type ^2})
Pythales a écrit:Je vois ton problème, mais je ne crois pas qu'on puisse trouver une formule générale pour. Il faut citer 3 coefficients successifs pour comprendre la loi de succession.
A titre de comparaison, si au lieu deet
on avait
et
, toutes choses égales par ailleurs, le développement serait
)
et là encore il n'est pas possible de donner une formule générale.
En utilisant la relation
Remarques.
On n'aura pas de problèmes de convergences pour
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : maths4ever et 68 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
