Fonction mesurable

par **xixxxxx** » 05 Juil 2013, 11:54

Bonjour,

Soit

un espace mesurable et

.

Alors je sais montrer que la fonction caractéristique

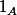
qui va de

dans

est mesurable.

Cependant je n'arrive pas à établir ce fait :

Soient

un partage fini de

qui est

-mesurable et

. Alors l'application

est mesurable.

Voilà ma tentative :

Soit

un borélien de

. Alors si j'arrive à démontrer qu'il existe

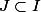
tel que

alors c'est gagné. Sauf que je ne sais pas comment démontrer cela.

Cordialement,

par **arnaud32** » 05 Juil 2013, 16:23

montre tout simplement que a*1_Ai et 1_A + 1_B sont mesurables et tu feras une recurence ensuite