Restrictions de fonction mesurable !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Nov 2007, 12:30
par barbu23 » 10 Nov 2007, 12:30
Bonjour :
proposition :Soient
 $)
et
 $)
deux espaces mesurables.
Soit
_{ n \geq 0} $)
une suite de parties de
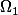
verifiant :
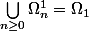
.
Soit

.

est
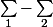
mesurable si et seulement si :
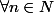
: la restriction
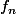
de

à
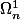
est
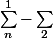
mesurable où :
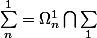
.
Preuve :Suppososns que

est
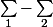
mesurable.
Considerons :
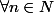
:
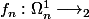
tel que :
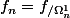
.
Montrons que :
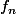
est
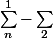
.
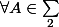
:
 = \Omega_{n}^{1} \bigcap f^{-1}(A) $)
.
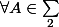
:
 \in \Omega_{n}^{1} \bigcap \sum_{1} = \sum_{n}^{1} $)
.
Donc :
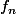
est
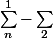
mesurable.
Suppososns maintenant que :
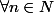
:
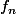
est
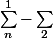
mesurable.
Montrons que :

est
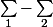
mesurable.
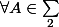
:
 = \Omega_{1} \bigcap f^{-1}(A) = ( \displaystyle \bigcup_{n \geq 0} \Omega_{n}^{1} ) \bigcap f^{-1}(A) = \displaystyle \bigcup_{ n \geq 0 } ( \Omega_{n} \bigcap f^{-1}(A) ) = {\displaystyle \bigcup_{ n \geq 0 }} f_{n}^{-1}(A) \in {\displaystyle \bigcup_{ n \geq 0 }} \sum_{n}^{1} \subset \sum_{1} $)
.
Donc :

est
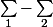
mesurable.
Questions : $)
ce que j'ai pas compris c'est : pourquoi
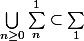
!!
Merci d'avance !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Nov 2007, 12:37
par barbu23 » 10 Nov 2007, 12:37
En fait :
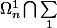
est la tribu induite par la tribu

sur
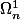
.
Comme pour le cas de la topologie induite !! bon ... !
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 10 Nov 2007, 12:43
par tize » 10 Nov 2007, 12:43
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Nov 2007, 12:48
par barbu23 » 10 Nov 2007, 12:48
D'accord ! merci beaucoup "tize" !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Nov 2007, 13:30
par barbu23 » 10 Nov 2007, 13:30
Bonjour :
Soit

la restriction de

à
 $)
est
 $)
mesurable
 $)
d'après un résultat dèjà vu .
Le resultat dèjà vue est celui cité au debut de ce fil !!
Pouvez vous m'expliquer quel rapport y'a-t-il entre ce "résultat dèjà vue " et
 $)
?
Merci d'avance !!
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 10 Nov 2007, 13:39
par tize » 10 Nov 2007, 13:39
Bonjour,
il suffit de prendre
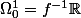)
et
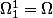
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Nov 2007, 14:04
par barbu23 » 10 Nov 2007, 14:04
tize a écrit:Bonjour,
il suffit de prendre
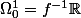)
et
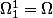
Attend "tize", j'ai pas vraiment bien compris :

:
 \longrightarrow ( \overline{\mathbb{R}} , \mathbb{B}(\overline{\mathbb{R}}} ) $)
On a :
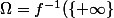 \bigcup f^{-1}(\{-\infty\}) \bigcup f^{-1}(\mathbb{R}) $)
Donc , il y'a

restrictions :
} $)
:
 , f^{-1} ( \{ + \infty \} ) \bigcap \sum ) \longrightarrow ( \overline{\mathbb{R}} , \mathbb{B}(\overline{\mathbb{R}}} ) $)
} $)
:
 , f^{-1} ( \{ - \infty \} ) \bigcap \sum ) \longrightarrow ( \overline{\mathbb{R}} , \mathbb{B}(\overline{\mathbb{R}}} ) $)
} $)
:
 , f^{-1} ( \{ \mathbb{R} \} ) \bigcap \sum ) \longrightarrow ( \overline{\mathbb{R}} , \mathbb{B}(\overline{\mathbb{R}}} ) $)
 $)
mais je comprends pas pourquoi
 $)
est
 $)
est mesurable !! en fait , elle est
 \bigcap \sum ) \hspace{10cm} - \mathbb{B}(\overline{\mathbb{R}}} $)
mesurable ? non ?
C'est ça ?!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Nov 2007, 16:30
par barbu23 » 10 Nov 2007, 16:30
Help pls !! :doh: :cry:
Merci d'avance !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Nov 2007, 16:59
par barbu23 » 10 Nov 2007, 16:59
"tize" , d'accord, j'ai vu ce que tu m'a écrit et c'est pratiquement la même chose si on garde
 $)
et

mais je vois pas pourquoi la restriction est
 $)
mesurable !!
Est ce que tu peux m'aider là ?!!
merci d'avance !!
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 10 Nov 2007, 17:04
par tize » 10 Nov 2007, 17:04
Désolé je ne comprend plus ce que tu veux montrer,
que f est
 $)
ou que
f est
 $)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Nov 2007, 17:16
par barbu23 » 10 Nov 2007, 17:16
Je veux montrer que la restriction de

à
 $)
est
 $)
mesurable !!
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 10 Nov 2007, 17:26
par tize » 10 Nov 2007, 17:26
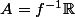\in\sum)
donc pour tout borélien

de
)
,
=A\bigcap f^{-1}\(B\)=f^{-1}\(B\))
(car
\subset A)
) donc
)
est mesurable pour tout borélien

donc
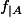
est
 $)
mesurable.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Nov 2007, 17:34
par barbu23 » 10 Nov 2007, 17:34
Merci beaucoup "tize" !
Est ce que la fonction définie par
 \longrightarrow sup(x,y) $)
est continue pour conclure à la fin qu'elle est mesurable !! et donc
 $)
est mesurable pour

et

mesurable !!
Merci d'avance !!
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
 par ThSQ » 10 Nov 2007, 17:40
par ThSQ » 10 Nov 2007, 17:40
barbu23 a écrit:Est ce que la fonction définie par
 \longrightarrow sup(x,y) $)
est continue
sup(x,y) = (|x-y| + x + y)/2 donc est C°
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Nov 2007, 17:42
par barbu23 » 10 Nov 2007, 17:42
D'accord, merci beaucoup !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Nov 2007, 18:23
par barbu23 » 10 Nov 2007, 18:23
Bonsoir :
Proposition:Toute fonction étagée
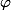
s'écrit sous la forme :
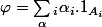
où :
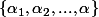
et
_{i=1,...,n} $)
est une partition mesurable de
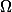
, c'est à dire :
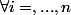
:
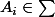
et
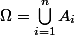
et
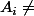
et
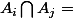
si :
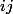
.
Preuve :Soit
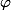
une fonction étagée avec :
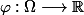
.
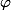
est
 $)
mesurable et
 = \{ \alpha_{1} , ... , \alpha_{n} \} \subset \mathbb{R} $)
...
Pour
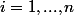
:
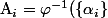 \in \sum $)
.
Si :
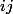
, supposons que :
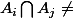
.
Alors :
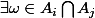

 = \alpha_{i} = \alpha_{j} $)
( contradiction )
Donc :
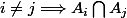
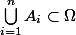
Réciproquement :
Soit
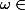
.
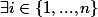
:
 = \alpha_{i} $)
.
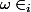

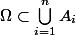 Questions :
Questions : $)
les passages que j'ai pas compris sont : pourquoi :
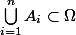
et
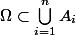
merci d'avance !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Nov 2007, 18:57
par barbu23 » 10 Nov 2007, 18:57
Hep pls ! :help: :cry:
Merci d'avance !!
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 10 Nov 2007, 19:16
par tize » 10 Nov 2007, 19:16
Et bien il est démontré que
pour tout 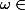
il existe
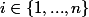
tel que
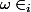
donc
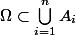
.
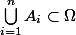
car les

sont tous des sous ensembles de

, leur union l'est donc aussi.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 10 Nov 2007, 20:45
par barbu23 » 10 Nov 2007, 20:45
Merci "tize" !!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 11 Nov 2007, 16:33
par barbu23 » 11 Nov 2007, 16:33
Bonjour :
Soit
_{n \geq 0} $)
une suite parties de

.
On note :
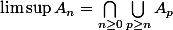
.
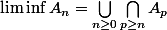
On suppose que la suite :
_{n \geq 0} $)
est croissante.
Il faut montrer que
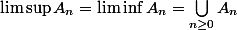
J'ai montré que :
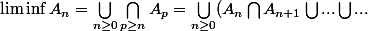 = \displaystyle \bigcup_{ n \geq 0} A_{n} $)
Mais pour
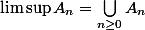
j'arrive pas !! pouvez vous m'aider ?
Merci d'avance !!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités