Fonction mesurable
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
road runner
- Membre Relatif
- Messages: 163
- Enregistré le: 05 Fév 2007, 18:35
-
 par road runner » 24 Jan 2008, 19:49
par road runner » 24 Jan 2008, 19:49
bonsoir
comment montrer qu'une fonction est mesurable ,j'ai compris comment faire (image reciproque d'un element qui engendre la tribu d'arrivé qui doit etre mesurable ..)mais comment le faire en réalité ?
par exemple
 = 2^n \text { si } 1/2^n \le x \le 1/2^{n-1})
et 0 sinon ?
merci d'avance
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 24 Jan 2008, 19:53
par tize » 24 Jan 2008, 19:53
Bonjour,
ta fonction est égale à

et

est mesurable, donc ...
-
road runner
- Membre Relatif
- Messages: 163
- Enregistré le: 05 Fév 2007, 18:35
-
 par road runner » 24 Jan 2008, 20:11
par road runner » 24 Jan 2008, 20:11
j'ai déja vu ca ,peux tu etre plus explcicite s'il te plait et juste me dire comment géneraliser ca .
merci encore
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 24 Jan 2008, 20:38
par tize » 24 Jan 2008, 20:38
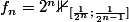
donc de toute manière pour tout ensemble mesurable

,
)
est soit égal à

soit

soit

soit

....
Ici c'est un cas particulier facile car une indicatrice d'un ensemble mesurable est toujours une fonction mesurable par suite une combinaison linéaire de celles ci est encore mesurable...
Dans les cas plus généraux, s'il s'agit de la tribu des boréliens, étant donné qu'elle est engendrée par les ouverts, il suffit de montrer que l'image réciproque d'un ouvert est un ouvert (on peut même se restreindre aux intervalles ouverts ou carrément à ceux du type
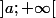
)...c'est en particulier le cas des fonctions continues puisque l'image réciproque d'un ouvert est un ouvert et donc une partie mesurable...
-
road runner
- Membre Relatif
- Messages: 163
- Enregistré le: 05 Fév 2007, 18:35
-
 par road runner » 24 Jan 2008, 20:57
par road runner » 24 Jan 2008, 20:57
merci de ton aide ,pour être sûre que j'ai copmpris
est ce que je pourais avoir une explication avec cette fonction
 = 1 \text { si } x \ge 0 \text { et } -1 { si } x < 0)
merci encore
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 24 Jan 2008, 21:26
par tize » 24 Jan 2008, 21:26
Le n ne sert à rien....Dans ce cas précis, c'est facile puisque
=\mathbb{1}_{[0;+\infty[}^{(x)}\;-\;\mathbb{1}_{]-\infty;0[}^{(x)})
... combinaison linéaire d'indicatrices de parties mesurables.
-
road runner
- Membre Relatif
- Messages: 163
- Enregistré le: 05 Fév 2007, 18:35
-
 par road runner » 24 Jan 2008, 21:52
par road runner » 24 Jan 2008, 21:52
c'est ca qu'il faut faire a chaque fois ? ,on essaye d'ecrire notre fonction comme combinaison lineaire de fonctions indicatrices ?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 24 Jan 2008, 21:59
par tize » 24 Jan 2008, 21:59
Non pas à chaque fois, et c'est des indicatrices de parties mesurables, toutes les fonctions mesurables ne sont évidemment pas combinaison linéaire de ces indicatrices, il y a d'autre méthodes comme je te l'ai écrit dans le message 4...
-
road runner
- Membre Relatif
- Messages: 163
- Enregistré le: 05 Fév 2007, 18:35
-
 par road runner » 24 Jan 2008, 22:06
par road runner » 24 Jan 2008, 22:06
oué sinon ca serait trop beau :we: ,
t'aurais pas un exemple d'une autre méthode a me donner s'il te plait ?
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 24 Jan 2008, 22:22
par tize » 24 Jan 2008, 22:22
Je sais pas trop en générale il y a de la continuité ou de la continuité par morceaux et on en déduit que la fonction est borélienne mais tu peux aussi essayer de montrer ces deux exemples importants :
si f et g sont mesurables alors h(x)=max(f(x),g(x)) est mesurable.
si la suite de fonctions mesurables fn -> f simplement alors f est mesurable.
-
road runner
- Membre Relatif
- Messages: 163
- Enregistré le: 05 Fév 2007, 18:35
-
 par road runner » 24 Jan 2008, 22:46
par road runner » 24 Jan 2008, 22:46
pour la premiere je crois que c'est bon ,mais est ce qu'il y'aurait pas une histoire de "presque partout" la ?
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 25 Jan 2008, 00:40
par Joker62 » 25 Jan 2008, 00:40
là une se fait en deux lignes avec max(x,y) = (|x-y|+(x+y))/2
Composée de fonctions mesurables.
Pour la deuxième question), je rajoute que si f est bornée, alors ça converge même uniformément :D
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 25 Jan 2008, 11:17
par tize » 25 Jan 2008, 11:17
Salut Joker :we: ,
je ne comprends pas ta remarque pour la 2),
j'ai dit si les fonctions mesurables fn -> f simplement alors f est mesurable.
Pourquoi f bornée implique-t-il la convergence uniforme ? C'est faux, non ? Il y a des contres exemples assez simples...ou alors je n'ai pas compris ta remarque...
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 25 Jan 2008, 13:16
par Joker62 » 25 Jan 2008, 13:16
Lol oui en effet, c'était nimps !!! :)
Je venais de faire le cours en fait, et j'avais pas encore relu ! :)
Donc le vrai truc c'était :
Si f est une fonction positive mesurable, alors on peut l'approximer par une suite de fonction étagées.
Et là, si f est majorée, alors cette suite de fonction converge uniformément.
Désolé encore
-
road runner
- Membre Relatif
- Messages: 163
- Enregistré le: 05 Fév 2007, 18:35
-
 par road runner » 25 Jan 2008, 16:57
par road runner » 25 Jan 2008, 16:57
bonjour ,je voudrais utiliser l'une des définitions de mesurable ,càd, (
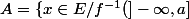 \} \text {mesurable})
quelque soit a ;
pour montrer que f est est mesurable ,comment m'y prendre ,?
je parle de f= 1 si x >= 0 et -1 si x<0
merci d'avance
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 25 Jan 2008, 17:45
par tize » 25 Jan 2008, 17:45
Bonjour,
fais un dessin dans ce cas là
)
ne peut être égal qu'à

,
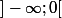
ou

-
road runner
- Membre Relatif
- Messages: 163
- Enregistré le: 05 Fév 2007, 18:35
-
 par road runner » 25 Jan 2008, 18:05
par road runner » 25 Jan 2008, 18:05
j'ai fait le dessin ,j'arrive à voir qu'on a trois cas pour a ,mais je n'arrive pas à voir ce que représente
)
pouvez vous m'aider s'il vous plait ,
merci encore
-
tize
- Membre Complexe
- Messages: 2385
- Enregistré le: 16 Juin 2006, 19:52
-
 par tize » 25 Jan 2008, 18:13
par tize » 25 Jan 2008, 18:13
Par définition :
=\{x\in\mathbb{R}\; ;\; f(x)\in]- \infty , a ]})
, tous les x de R dont l'image par f est inférieur ou égal à "a".
-
road runner
- Membre Relatif
- Messages: 163
- Enregistré le: 05 Fév 2007, 18:35
-
 par road runner » 25 Jan 2008, 18:46
par road runner » 25 Jan 2008, 18:46
ok c'est bon ,
est ce la meme chose pour la suite fn définie plus haut ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités