Equation de second degré bac
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
vt0388
- Messages: 4
- Enregistré le: 19 Fév 2013, 21:47
-
 par vt0388 » 10 Juin 2013, 14:55
par vt0388 » 10 Juin 2013, 14:55
Bonjour, je passe le bac sti2d dans une semaine et en voulant m'entrainer je tombe sur une equation de second degré que je n'arrive pas a comprendre, voilà l'énoncé et la correction :

Je trouve un dicriminant de -64, donc négatif, l'équation n'est pas censé ne pas avoir de solutions lorsque le discriminant est négatif ?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 10 Juin 2013, 14:57
par Sylviel » 10 Juin 2013, 14:57
Bonjour,
effectivement il n'y a pas de solution réelles. en revanche il y a des solutions complexes (il suffit de faire comme si V(-64)=i V(64) ) comme indiqué sur le lien que tu nous as fournis.
Je ne sais pas si les complexes étaient à ton programme par contre...
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
vt0388
- Messages: 4
- Enregistré le: 19 Fév 2013, 21:47
-
 par vt0388 » 10 Juin 2013, 15:00
par vt0388 » 10 Juin 2013, 15:00
Ok, je galère un peu entre solutions réelles/complexes, merci de la réponse :)
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 10 Juin 2013, 15:05
par Sylviel » 10 Juin 2013, 15:05
Une manière de faire est de te dire que tu as toujours des solutions complexes (en considérant que V(-1)=i, même s'il vaut mieux ne pas l'écrire pour diverse raisons). Parfois ces solutions complexes sont réelles (si le discriminant est positif par exemple).
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
vt0388
- Messages: 4
- Enregistré le: 19 Fév 2013, 21:47
-
 par vt0388 » 10 Juin 2013, 15:10
par vt0388 » 10 Juin 2013, 15:10
J'ai du mal a comprendre d'où sort le : (8i)² dans la correction ...
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 10 Juin 2013, 15:13
par Sylviel » 10 Juin 2013, 15:13
Schématiquement :
V(-64) = V(-1) * V(64) = i * 8 = 8i
Rigoureusement :
tu as dans ton cours que, si Delta <0, alors les racines sont
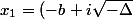/2a)
et
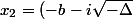/2a)
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
vt0388
- Messages: 4
- Enregistré le: 19 Fév 2013, 21:47
-
 par vt0388 » 10 Juin 2013, 15:18
par vt0388 » 10 Juin 2013, 15:18
Ah ok, je comprend maintenant, c'est vrai que i² = -1, merci beaucoup, je peux me remettre au travail :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités

