Le cercle
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
andik07
- Messages: 7
- Enregistré le: 01 Juin 2013, 17:57
-
 par andik07 » 01 Juin 2013, 22:27
par andik07 » 01 Juin 2013, 22:27
J´ai besoin d´aider avec cet exercice... je ne sais pas du tout ce qu´il faut faire!
Soit A(1, 2), B(-1, 2), C(3, 4).
Déterminer le centre et le rayon du cercle K de diametre AB.
Donner une équation du cercle K.
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 01 Juin 2013, 22:42
par annick » 01 Juin 2013, 22:42
Bonjour,
Déjà, tu peux trouver les coordonnées du centre du cercle puisque tu connais sont diamètre [AB].
Tu peux ensuite calculer la mesure de KA ou de KB, donc tu connaitras la valeur du rayon.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 01 Juin 2013, 22:51
par Ericovitchi » 01 Juin 2013, 22:51
Et pour l'équation du cercle tu peux aussi écrire que le produit scalaire
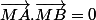
(en faisant XX'+YY'=0 et avec M étant un point courant du cercle M(x;y) )
(mais sinon tu peux évidemment écrire que MO²=R² si tu as déjà calculé le rayon, O étant le centre du cercle)
-
andik07
- Messages: 7
- Enregistré le: 01 Juin 2013, 17:57
-
 par andik07 » 01 Juin 2013, 22:56
par andik07 » 01 Juin 2013, 22:56
mais comment calculer les coordonnées du centre du cercle svp?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 01 Juin 2013, 22:57
par Ericovitchi » 01 Juin 2013, 22:57
il est au milieu de AB donc utilise les formules qui donne le milieu d'un segment (la demi somme des abscisses et des ordonnées).
-
andik07
- Messages: 7
- Enregistré le: 01 Juin 2013, 17:57
-
 par andik07 » 01 Juin 2013, 23:05
par andik07 » 01 Juin 2013, 23:05
j´ai trouvé 0, 2.... c´ect bien? et je continue comment?
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 01 Juin 2013, 23:10
par annick » 01 Juin 2013, 23:10
Ok pour les coordonnées de K.
Pour calculer le rayon tu calcules KA avec la formule de la longueur d'un segment :
MN=V((xN-xM)²+(yN-yM)²) (V veut dire racine carrée de...)
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 01 Juin 2013, 23:15
par annick » 01 Juin 2013, 23:15
Pour l'équation du cercle plusieurs méthodes :
1) celle d'Ericovitchi
2) KM=R qui s'écrit aussi KM²=R² (vu la valeur simple de R ici, c'est une méthode facile)
3) Tu connais la forme générale de l'équation du cercle : (x-a)²+(y-b)²=R² dont le centre a pour coordonnées (a,b)
-
andik07
- Messages: 7
- Enregistré le: 01 Juin 2013, 17:57
-
 par andik07 » 01 Juin 2013, 23:19
par andik07 » 01 Juin 2013, 23:19
c´est combien K? pour calculer KA?
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 01 Juin 2013, 23:22
par annick » 01 Juin 2013, 23:22
Je t'ai dit que j'étais d'accord avec tes coordonnées K(0,2), donc je trouve bizarre que tu me redemandes "c'est combien K".
-
andik07
- Messages: 7
- Enregistré le: 01 Juin 2013, 17:57
-
 par andik07 » 01 Juin 2013, 23:32
par andik07 » 01 Juin 2013, 23:32
oui, c´est vrai... désolé, c´est peut etre parce que j´suis un peu fatigué et je fais les math depuis l´aprem
-
andik07
- Messages: 7
- Enregistré le: 01 Juin 2013, 17:57
-
 par andik07 » 01 Juin 2013, 23:37
par andik07 » 01 Juin 2013, 23:37
le rayon est alors racine de 1?
-
andik07
- Messages: 7
- Enregistré le: 01 Juin 2013, 17:57
-
 par andik07 » 01 Juin 2013, 23:56
par andik07 » 01 Juin 2013, 23:56
et l´équation du cercle est x2+y2-4y+3=0??
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 02 Juin 2013, 07:16
par annick » 02 Juin 2013, 07:16
andik07 a écrit:le rayon est alors racine de 1?
Et que vaut V1 ?
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 02 Juin 2013, 07:22
par annick » 02 Juin 2013, 07:22
andik07 a écrit:et l´équation du cercle est x2+y2-4y+3=0??
Oui, ton équation de cercle est juste. On peut d'ailleurs vérifier que les coordonnées de A et de B vérifient bien l'équation du cercle.
Bonne journée à toi.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
